[ Takaisin pääsivulle | Back to main page ]

Esimerkki 2

Tutkitaan luonnollista äänisignaalia ja syntetisoitua determinististä signaalia.

perusjakso T0: lyhin jaksonaika, jonka välein signaali toistaa itseään, x(t) == x(t+T0), [T0] = sekunti. Englanniksi "fundamental period" tai "basic period" tai "primitive period" jne. Katso matematiikan kirjasta "Fourier series"!

perustaajuus f0: taajuus, jonka avulla kaikki muuta signaalin taajuudet voidaan esittää sen monikertoina, [f0] = Hertz. Englanniksi "fundamental frequency" tai "basic frequency", äänisignaalista puhuttaessa useimmiten "pitch".

Yhteys: f0 = 1/T0, T0 = 1/f0.

Ääninäyte

Tutkitaan tutkija Sampsa Laineen ilmoille kajauttamaa ääninäytettä [ WAV (190 kB) ]. Siinä hän sanoo piiiitkän vokaaliäänteen. Sen aaltomuotoa on esitetty kuvassa 1. Huomaa, että kuvassa on vain pieni jakso, joka on hyvin jaksollisen näköinen (kvasijaksollinen, quasi-periodic), mutta jossa kuitenkin näkyy pientä vaihtelua.

Tehtävä: Arvioi kuvan perusteella jaksonaika T0. Voit laskea yhteen usemman jakson ajan ja jakaa lopputuloksen jaksojen määrällä. (Jaksonaika on 0.001 ja 0.01 sekunnin välissä. Oikean vastauksen voi katsoa sivun alaosan linkistä.)

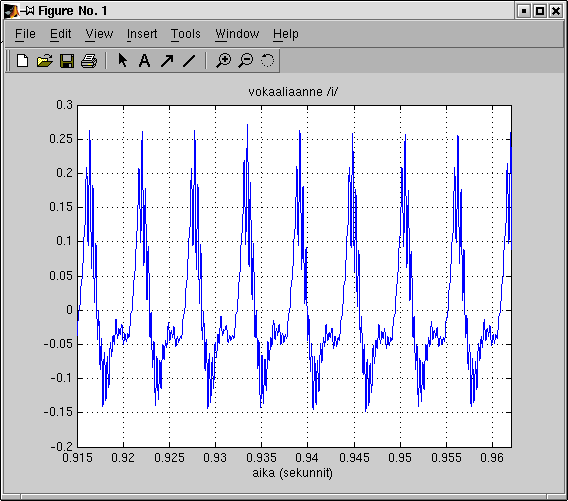
input-signaali
Kuva 1: Signaali aikatasossa. Vokaaliäänteen /i/ aaltomuoto noin viiden sadasosasekunnin ajalta.

Otetaan kyseisestä signaalista Fourier-muunnos eli tarkastellaan, mistä komponenteista signaali muodostuu. Jaksollisen signaalin Fourier-sarjaesitys on:

x(t) = SUMMA a_k exp(j 2 pi f_0 k t)

jossa summaus k-indeksiä käyttäen käy miinus äärettömästä äärettömään, a_k on Fourier-kertoimet ja f_0 on perustaajuus (PDF-dokumentissa selkeämmin kaava). Piirretään spektri kuvaan 2. Piikki spektrissä tarkoittaa sen taajuista kosinisignaalia aikatason esityksessä. Mitä korkeampi piikki, sitä suurempi amplitudi kyseisellä kosinikomponentilla on.

Tehtävä: Arvioi kuvan 2 perusteella perustaajuus f0. Perustaajuus on se taajuus, jonka avulla kaikki muut taajuudet voidaan esittää sen monikertoina. Tässä tapauksessa perustaajuus on siis ensimmäinen piikki noin 100 .. 200 Hz:n välissä. Yhtälailla sama taajuus löytyy jokaisen piikin erona, joten voit jälleen laskea usemman piikin yli taajuuden jakaa lopputuloksen komponenttien määrällä. Spektrin perustaajuus ei välttämättä/useinkaan ole sen korkein piikki!!! (Tässä tapauksessa sattuu olemaan.) Perustaajuutta ei välttämättä tarvitse esiintyä signaalissa!!! Esimerkiksi x(t) = cos(2pi 1000 t) + cos(2pi 1500 t), perustaajuus f0 = 500, koska x(t) = cos(2pi 2*500 t) + cos(2pi 3*500 t). (Tässä tapauksessa perustaajuus sattuu olemaan mukana.)

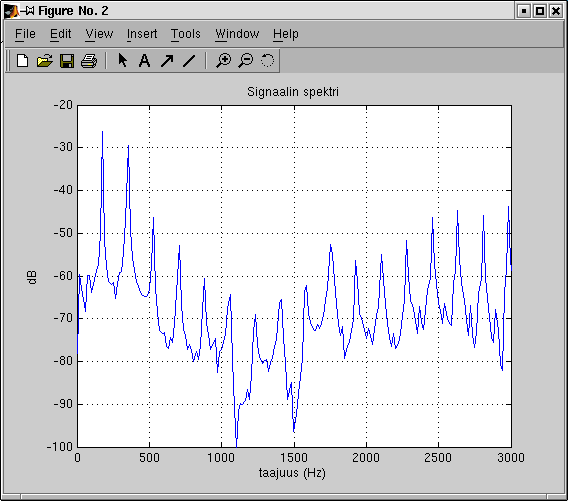
Signaalin spektri dB-asteikolla
Kuva 2: Signaalin spektri. X-akselilla on taajuus 0 .. 3000 Hz, ja Y-akselilla voimakkuus logaritmisella desibeliasteikolla.

Jaksonajan ja taajuuden yhteys

Kosini cos(2 pi f t) värähtelee f kertaa sekunnin aikana. Jos f=2, niin se värähtelee kaksi kertaa. Tällöin jaksonaika on T=0.5.

Tehtävä: Mikä on perusjakson T ja perustaajuuden f0 yhteys? Tarkista kuvaajista 1 ja 2 saatujen arvojen oikeellisuus.

Yksittäisten komponenttien merkitys

PDF-dokumentissa esitetään, kuinka signaalin aaltomuoto lähestyy alkuperäistä, kun siihen yksitellen lisätään kosinikomponentteja matalimmista lähtien.

Linkkejä


[ Takaisin pääsivulle | Back to main page ]

http://www.cis.hut.fi/Opinnot/T-61.246/Demo/esim2.shtml
t61246@cis.hut.fi
Friday, 22-Feb-2008 21:02:38 EET