[ Takaisin pääsivulle | Back to main page ]

Esimerkki 9

Liikkuva keskiarvoistava suodin. / Moving Average Filter.

Keskiarvoistaminen

Tutkitaan hyvin yksinkertaista laskuoperaatiota, jossa lukujonosta otetaan kaksi (N) vierekkäistä pistettä, lasketaan yhteen ja jaetaan kahdella (N). Kysymyksessä on siis aritmeettinen keskiarvo kahdella (N) pisteellä. Keskiarvoistamista voitaisiin jatkaa ottamalla esimerkiksi keskiarvo 7 pisteen yli (esim. viikkokeskiarvo). Voidaan helposti ajatella, että tämä operaatio jollain tavalla vähentää nopeita muutoksia. Toisaalta jos syötearvot ovat vakioita, myöskin keskiarvo on sama vakio.

Differenssiyhtälö

Olkoon laskettava suure lukujonossa x[n] ja keskiarvon laskennan tulos tulee y[n]:ään. Tällöin laskentaa kuvaava differenssiyhtälö on:

y[n] = 0.5 (x[n] + x[n-1])

tai vastaavasti

y[n] = 0.5 x[n] + 0.5 x[n-1]

Impulssivaste ja virtauskaavio

Differenssiyhtälön perusteella voidaan piirtää signaalinkäsittelyssä tyypillinen virtauskaavio (lohkokaavio), jossa D-neliö viittaa muistielementtiin.

tai ottamalla kerroin 0.5 eteen

Tästä saadaan helposti suotimen impulssivasteeksi h[n] = 0.5 (delta[n] + delta[n-1]).

Laskenta

Juoksevaa keskiarvoa voidaan laskea esimerkiksi näin:

k := 0;
while TRUE
  k    := k+1;
  y(k) := (x(k) + x(k-1))/2;
end;

Toisaalta, jos ajatellaan keskiarvoistaminen yllä piirrettynä suotimena, jonka impulssivaste h[n] tunnetaan, saadaan suodatuksen tulos y[n] konvoluutiona syötteestä x[n] ja impulssivasteesta h[n]:

y[n] = h[n] * x[n]
     = SUMMA_k  h[k] x[n-k]

missä * on konvoluutio-operaatio.

Suotimen taajuusominaisuudet

Signaalinkäsittelyssä tarkkaaillaan niin signaaleja kuin järjestelmiä sekä aika- että taajuustasossa. Tutkitaan seuraavaksi, miltä suotimen taajuusominaisuudet ovat.

Käytetään Fourier-muunnosta ja saadaan

H(e^jw) = H(exp(jw)) = 0.5 (1 + exp(-jw))
                     = 0.5 (1 + (cos(w) - j sin(w)))
                     = [0.5 + 0.5 cos(w)] - j [0.5 sin(w)]

Tämä on siis kompleksiarvoinen funktio, jossa w on reaalinen ja saa arvoja 0..pi. Kun lasketaan |H(e^jw)|, havaitaan että pienillä w:n arvoilla arvo on lähellä ykköstä pienentyen monotonisesti nollaan kohdassa w=pi. Näin ollen suodin on alipäästösuodin.

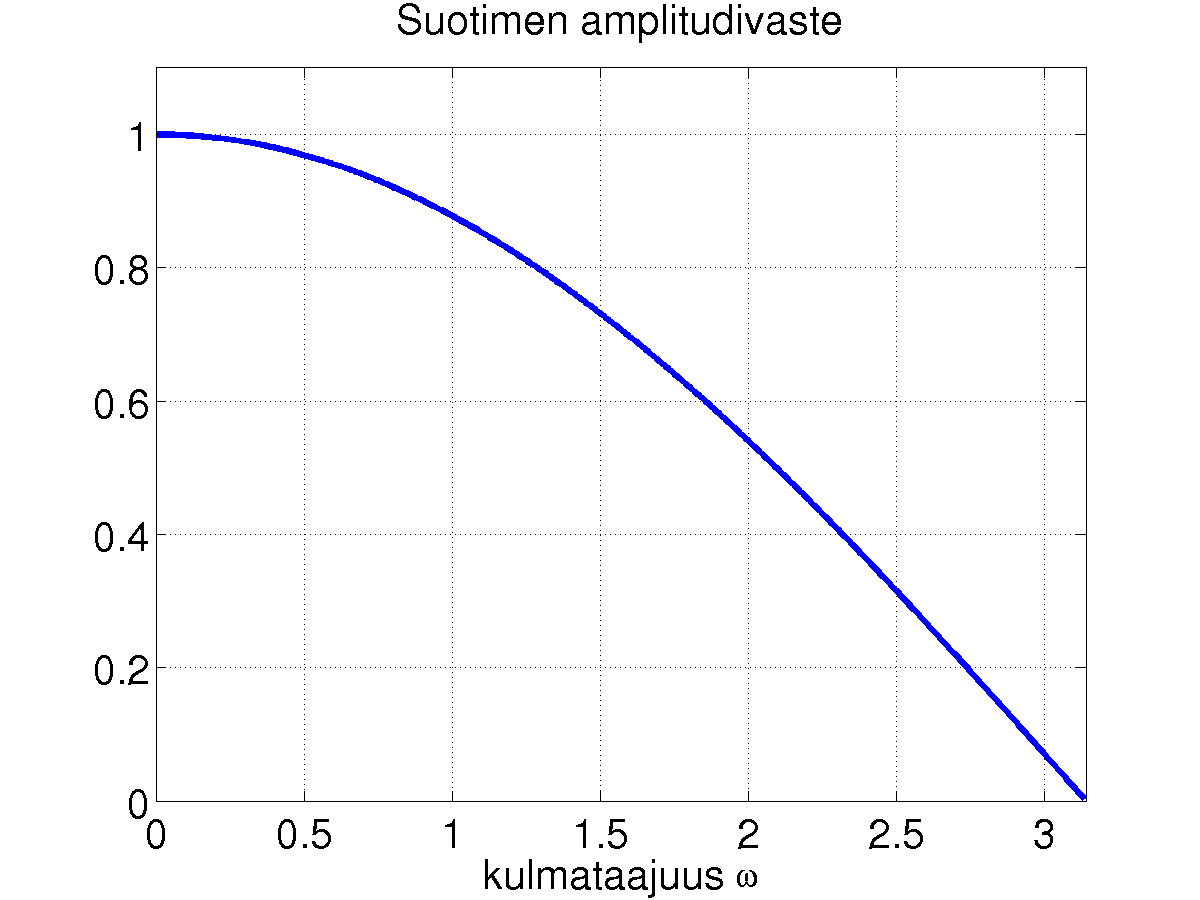
Vastaava voidaan ajatella myös napanollakuviosta. Käytetään apuna Z-muunnosta ja saadaan

H(z) = 0.5 (1 + z^-1) = 0
       0.5 z + 0.5    = 0
       z              = -1

Suodatusesimerkki

Otetaan dataa ja suodatetaan sitä tällä keskiarvoistavalla suotimella. Oheisessa kuvassa sininen on alkuperäinen ja punainen suodatettu käyrä. Huomataan, että nopeat muutokset (=korkeat taajuudet) ovat vähentyneet!

Tehtävä

Suodatusta voidaan tehostaa ottamalla aritmeettista keskiarvoa useammasta kuin kahdesta näytteestä. Esimerkiksi seitsemästä päivälämpötilasta voidaan saada viikkolämpötila.

Piirrä virtauskaavioesitys, kirjoita differenssiyhtälö ja impulssivaste sekä koodinpätkä laskemaan seitsemän pisteen keskiarvoistavaa suodinta.

Vastauksia täällä.

[ Takaisin pääsivulle | Back to main page ]

http://www.cis.hut.fi/Opinnot/T-61.246/Demo/esim9.shtml
t61246@cis.hut.fi
Friday, 27-Aug-2004 13:28:34 EEST