T-61.5020 Statistical Natural Language Processing
Exercises 10 -- Speech recognition and language model evaluation
Version 1.0

1.

Consider a simple phonetic model presented in Figure 1. The model has five states, $S_1, \ldots, S_5$, of which $S_1$ is both initial and final state. Every edge between the states has a transition probability $a_{ij} = P(S_j \vert S_i)$. The edges that are not drawn in the figure have a zero probability. In addition, each existing edge has also a character corresponding to the phoneme that is emitted, and a emission distribution for the acoustic features $o_k$: $b_{ij}(o_k) = P(o_k \vert S_i \to S_j)$. An exception is the edges that lead to the first state: Those are so-called epsilon or null transitions that have no emissions, and correspond to word breaks.

Figure 1: Phonetic model.

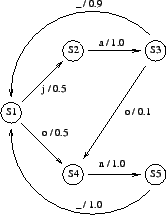
We have a speech signal from which we have calculated the feature vectors $o_1, \ldots, o_4$. In Table 1 there are emission probabilities of the edges for each vector.

Table 1: Emission probabilities $b_{ij}(o_k)$.

$i,j$	$o_1$	$o_2$	$o_3$	$o_4$
1,2	$10^{-1}$	$10^{-2}$	$10^{-3}$	$10^{-3}$
2,3	$10^{-3}$	$10^{-1}$	$10^{-1}$	$10^{-3}$
3,4	$10^{-3}$	$10^{-1}$	$10^{-1}$	$10^{-4}$
4,5	$10^{-3}$	$10^{-4}$	$10^{-3}$	$10^{-1}$
1,4	$10^{-3}$	$10^{-2}$	$10^{-2}$	$10^{-4}$

a)

Find the most probable state sequence using the Viterbi algorithm. The sequence should start and end with state 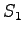$S_1$. What word or word sequence is obtained?

b)

Let's utilize a language model for the recognition task. The relevant probabilities are the following:

$$\begin{array}{lcclcclcc} P(\textrm{ja}) & = & 10^{-2} & P(\... ... \\ P(\textrm{jaon}) & = & 10^{-5} & & & & & & \\ \end{array}$$

Again, find the most probable state sequence and the corresponding word(s). Note that the path of the Viterbi algorithm must be calculated separately for all possible words. Multiply the language model probability to the estimates every time a new word is selected.

2.

Comparison of different language models may not be straightforward, especially if the models utilize separate sets of model units. Let's examine how it can be done.

Assume that we have trained two different statistical word segmentations, A and B, from a training corpus. Using the same corpus, we have trained three language models of different size for the units of both segmentations. The sizes are the numbers of n-grams in the models. From a separate 100000 word evaluation corpus we have calculated tokenwise cross-entropies for all of the models. The results are presented in Table 2.

Table: Cross-entropy results. Evaluation corpus consisted of 100000 words.

	Tokens		Cross-entropy 1		Cross-entropy 2		Cross-entropy 3
	types	in corpus	$H_M$	size	$H_M$	size	$H_M$	size
Model A	2114	344960	4.54	472227	4.39	664601	4.31	998907
Model B	6535	301271	5.19	518286	5.02	712133	4.93	1049750

In addition, the models have been tested in a speech recognition system. The recognition results are evaluated with word error rate (WER), which is the percentage of words recognized incorrectly. The results are in Table 3.

Table 3: Speech recognition results.

	Recognition 1		Recognition 2		Recognition 3
	model size	WER	model size	WER	model size	WER
Model A	472227	17.64	664601	15.04	998907	14.25
Model B	518286	17.54	712133	15.01	1049750	13.97

Find out which one of the segmentations work better based on the cross-entropy and speech recognition results. How reliable conclusions can be made based on this data?