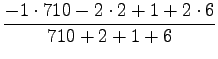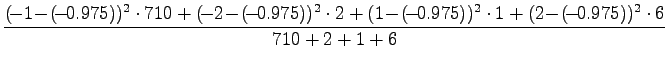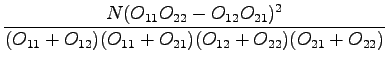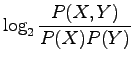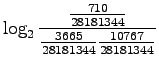- Frequency: Bigrams ``valkoinen'',''talo'' occurred
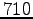 times.
times.
- Normalized frequence: Word ``valkoinen'' occurred
3665 times and ``talo'' 10767 times. We get
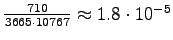 .
.
|
|
|
Normalized frequency
|
| liukas | keli | 1981 |
| aste | pakkanen | 386 |
| heittää | veivi | 293 |
| herne | nenä | 268 |
| valkoinen | talo | 180 |
| tuntematon | sotilas | 163 |
| vihainen | mielenosoittaja | 68 |
| kova | tuuli | 35 |
| ottaa | onki | 21 |
| venäjä | presidentti | 10 |
| oppia | lukea | 8 |
| hakea | työ | 1 |
| olla | ula | 0 |
| sekä | myös | 0 |
| ja | olla | 0 |
We see that results are quite good even for as simple method as this.
Rest of the results, sorted by the variance, are in Table 3.
|
|
|
Mean | Variance |
| herne | nenä | -1.000 | 0.000 |
| vihainen | mielenosoittaja | -1.000 | 0.000 |
| tuntematon | sotilas | -1.025 | 0.025 |
| valkoinen | talo | -0.975 | 0.083 |
| ottaa | onki | -1.250 | 0.188 |
| venäjä | presidentti | -1.128 | 0.472 |
| kova | tuuli | -0.880 | 0.492 |
| liukas | keli | -0.788 | 0.608 |
| oppia | lukea | -0.606 | 1.087 |
| heittää | veivi | -0.500 | 1.250 |
| aste | pakkanen | -0.465 | 1.347 |
| hakea | työ | -0.433 | 2.046 |
| olla | ula | -0.250 | 2.438 |
| sekä | myös | 0.252 | 2.981 |
| ja | olla | -0.083 | 3.635 |
This method has found in practice all the fixed collocations. However, results are not so good with sparse data: ``vihainen mielenosoittaja'' is definitely not a collocation.
Size of the window surely affects the results. If it is too large, pairs start to occur together randomly too often, if too small, the collocations with longer effect are not found. If the second word of the collocation can be either before or after the first one, the method will clearly not work at all.
In t-test we assume that the probabilities are normally distributed, and check if the expectation value for the observed data differs from the expectation value given by the null hypothesis. The t-values are given by
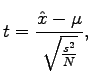 |
where
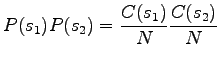 |
|||
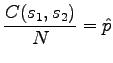 |
|||
For the pair ``valkoinen talo'' we get
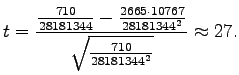 |
If the t-value is over 6.314, the probability that the sample was
from the distribution given by the independence assumption is
less than 5%. Consequently, we can mark ``valkoinen talo'' as
a collocation. Table 4 has values for all of the
candidates. Note that the last pairs get negative values. This
is because they occur together more rarely than the null hypothesis
gives.
![]() -test is based on a simple assumption: We look at the separate
probabilities and estimate how many times the words should occur together.
This is compared to the observed co-occurrence value, and if they differ
too much, the pair is likely to be a collocation.
-test is based on a simple assumption: We look at the separate
probabilities and estimate how many times the words should occur together.
This is compared to the observed co-occurrence value, and if they differ
too much, the pair is likely to be a collocation.
Let's start by collecting the following table (table 5):
These values can be used in the two-variable
By assigning the numbers:
If the result for
|
|
|
|
| liukas | keli | 591591 |
| valkoinen | talo | 358771 |
| aste | pakkanen | 173726 |
| tuntematon | sotilas | 70409 |
| ja | olla | 29194 |
| kova | tuuli | 26644 |
| venäjä | presidentti | 18147 |
| heittää | veivi | 4120 |
| herne | nenä | 2258 |
| vihainen | mielenosoittaja | 1321 |
| ottaa | onki | 525 |
| oppia | lukea | 449 |
| hakea | työ | 47 |
| sekä | myös | 45 |
| olla | ula | 0 |
The rest of the results are in Table 7.
|
|
|
MI |
| liukas | keli | 12.4 |
| aste | pakkanen | 10.1 |
| heittää | veivi | 9.7 |
| herne | nenä | 9.6 |
| valkoinen | talo | 9.0 |
| tuntematon | sotilas | 8.8 |
| vihainen | mielenosoittaja | 7.6 |
| kova | tuuli | 6.6 |
| ottaa | onki | 5.9 |
| venäjä | presidentti | 4.8 |
| oppia | lukea | 4.5 |
| hakea | työ | 1.7 |
| olla | ula | 0.5 |
| sekä | myös | -0.8 |
| ja | olla | -2.5 |
The results seem to be good. The course book criticises that this method favours the less frequent words. Reason for this is the way that is used to estimate the probabilities, i.e. maximum likelihood estimation. Better result can be obtained if we instead set a prior for the words to be independent, and let the data modify it.