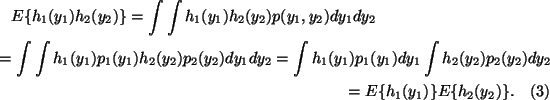Definition and fundamental properties

To define the concept of independence, consider two scalar-valued random variables y₁ and y₂. Basically, the variables y₁and y₂ are said to be independent if information on the value of y₁ does not give any information on the value of y₂, and vice versa. Above, we noted that this is the case with the variables s₁, s₂ but not with the mixture variables x₁, x₂.

Technically, independence can be defined by the probability densities. Let us denote by p(y₁,y₂) the joint probability density function (pdf) of y₁ and y₂. Let us further denote by p₁(y₁) the marginal pdf of y₁, i.e. the pdf of y₁ when it is considered alone:

$$p_1(y_1)=\int p(y_1,y_2) dy_2,$$ (7)

and similarly for y₂. Then we define that y₁ and y₂ are independent if and only if the joint pdf is factorizable in the following way:

 

p(y₁,y₂)=p₁(y₁)p₂(y₂). (8)

This definition extends naturally for any number n of random variables, in which case the joint density must be a product of n terms.

The definition can be used to derive a most important property of independent random variables. Given two functions, h₁ and h₂, we always have

$$E\{h_1(y_1) h_2(y_2)\}=E\{h_1(y_1)\}E\{h_2(y_2)\}.$$ (9)

This can be proven as follows:
$$\begin{multline}E\{h_1(y_1) h_2(y_2)\}=\int \int h_1(y_1) h_2(y_2)p(y_1,y_2) dy_... ...) dy_1 \int h_2(y_2)p_2(y_2) dy_2 \\ =E\{h_1(y_1)\}E\{h_2(y_2)\}. \end{multline}$$