

Next: Defining ICA by Mutual
Up: Minimization of Mutual Information
Previous: Minimization of Mutual Information
Using the concept of differential entropy, we define
the mutual information I between m (scalar) random variables,
yi,
i=1...m as follows
 |
(24) |
Mutual information is a natural measure of the dependence between
random variables. In fact, it is equivalent to the well-known
Kullback-Leibler divergence between the joint density
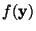 and the
product of its marginal densities; a very natural measure for
independence. It is always non-negative, and zero if and only if the
variables are statistically independent.
Thus, mutual information takes into
account the whole dependence structure of the variables, and not only
the covariance, like PCA and related methods.
and the
product of its marginal densities; a very natural measure for
independence. It is always non-negative, and zero if and only if the
variables are statistically independent.
Thus, mutual information takes into
account the whole dependence structure of the variables, and not only
the covariance, like PCA and related methods.
Mutual information can be interpreted by using the interpretation of
entropy as code length. The terms H(yi) give the lengths of codes
for the yi when these are coded separately, and
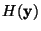 gives the
code length when
gives the
code length when 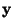 is coded as a random vector, i.e. all the
components are coded in the same code. Mutual information thus shows
what code length reduction is obtained by coding the whole vector
instead of the separate components. In general, better codes can be
obtained by coding the whole vector. However, if the yi are independent,
they give no information on each other, and one could just as well
code the variables separately without increasing code length.
is coded as a random vector, i.e. all the
components are coded in the same code. Mutual information thus shows
what code length reduction is obtained by coding the whole vector
instead of the separate components. In general, better codes can be
obtained by coding the whole vector. However, if the yi are independent,
they give no information on each other, and one could just as well
code the variables separately without increasing code length.
An important property of mutual information [36,8] is that we
have for an
invertible linear transformation
 :
:
 |
(25) |
Now, let us consider what happens if we constrain the yi to be uncorrelated and of unit variance.
This means
 ,
which implies
,
which implies
 ,
and this implies that
,
and this implies that
 must be
constant. Moreover, for yi of unit variance,
entropy and negentropy differ only by a constant, and the sign.
Thus we obtain,
must be
constant. Moreover, for yi of unit variance,
entropy and negentropy differ only by a constant, and the sign.
Thus we obtain,
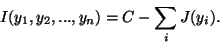 |
(26) |
where C is a constant that does not depend on 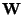 .
This shows the fundamental relation between negentropy and mutual
information.
.
This shows the fundamental relation between negentropy and mutual
information.


Next: Defining ICA by Mutual
Up: Minimization of Mutual Information
Previous: Minimization of Mutual Information
Aapo Hyvarinen
2000-04-19

![]() gives the
code length when
gives the
code length when ![]() is coded as a random vector, i.e. all the
components are coded in the same code. Mutual information thus shows
what code length reduction is obtained by coding the whole vector
instead of the separate components. In general, better codes can be
obtained by coding the whole vector. However, if the yi are independent,
they give no information on each other, and one could just as well
code the variables separately without increasing code length.
is coded as a random vector, i.e. all the
components are coded in the same code. Mutual information thus shows
what code length reduction is obtained by coding the whole vector
instead of the separate components. In general, better codes can be
obtained by coding the whole vector. However, if the yi are independent,
they give no information on each other, and one could just as well
code the variables separately without increasing code length.
![]() :
: