Conclusions

This paper surveyed contrast functions and algorithms for ICA. ICA is a general concept with a wide range of applications in neural computing, signal processing, and statistics. ICA gives a representation, or transformation, of multidimensional data that seems to be well suited for subsequent information processing. This is because the components in the representation are 'as independent as possible' from each other, and at the same time 'as non-Gaussian as possible'. The transformation may also be interesting in its own right, as in blind source separation.

In the discussion of the many methods proposed for ICA, it was shown that the basic choice of the ICA method seems to reduce to two questions. First, the choice between estimating all the independent components at the same time, and estimating only a subset of them, possibly one-by-one. Most ICA research has concentrated on the first option, but in practice, it seems that the second option is very often more interesting, due to computational and other considerations. Second, one has the choice between adaptive algorithms and batch-mode (or block) algorithms. Again, most research has concentrated on the former option, although in many applications, the latter option seems to be preferable, again for computational reasons.

In spite of the large amount of research conducted on this basic problem by several authors, this area of research is by no means exhausted. It may be that the estimation methods of the very basic ICA model are so developed that the probability of new breakthroughs may not be very large. However, different extensions of the basic framework provide important directions for future research, for example:

1.

Estimation of the noisy ICA model [31,43,63,66,107], as well as estimation of the model with overcomplete bases (more independent components than observed mixtures) [118,99,69], are basic problems that seem to require more research.

2.

Methods that are tailor-made to the characteristics of a given practical application may be important in many areas. For example, in some cases it would be useful to be able to estimate a model which is similar to the ICA model, but the components are not necessarily all independent. Exact conditions that enable the estimation of the model in that case would be interesting to formulate. Steps in this direction can be found in [25,70].

3.

The problem of overlearning in ICA has been recently pointed out [76]. Avoiding and detecting overlearning is likely to be of great importance in practical applications.

4.

If the 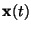${\bf x}(t)$ come from a stochastic process, instead of being a sample of a random variable, blind source separation can also be accomplished by methods that use time-correlations [135,16,105]. Integrating this information in ICA methods may improve their performance. An important extension of ordinary ICA contrast functions for this case was introduced in [119], in which it was proposed that Kolmogorov complexity gives a meaningful extension of mutual information.

5.

When ICA is used for blind separation of stochastic processes, there may also be time delays. This is the case if the signals propagate slowly from the physical sources to the sensors; because the distances between the sensors and the sources are not equal, the signals do not reach the sensors at the same time. This happens, e.g., in array processing of sound signals. A related problem in blind source separation is echos. Due to these phenomena, some kind of blind deconvolution must be made together with blind source separation, see e.g. [41,123,137,149,150,134,92].

6.

Finally, non-linear ICA is a very important, though at the same time an almost intractable problem. In neural networks as well as in statistics, several non-linear methods have been developed [90,52,55,17], and it may be possible to apply some of these to ICA. For example, in [120], the Self-Organizing Map [90] was used for non-linear ICA of sub-Gaussian independent components. This approach was generalized in [121] by using the generative topographic mapping [17]. Also the identifiability of non-linear ICA models needs further research; some results appeared in [75,133]. Other work can be found in [39,97].