

Next: Bibliography
Up: Survey on Independent Component
Previous: Definition of Cumulants
PCA: Principal Component Analysis
ICA: Independent Component Analysis
pdf: probability density function
Variables and constants:
i: General-purpose index, also: imaginary unit
m: Dimension of the observed data
n: Dimension of the transformed component vector
t: Time or iteration index
x and y: General-purpose scalar random variables
yi: Output of the i-th neuron in a neural network
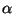 :
A scalar constant
:
A scalar constant
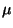 :
Learning rate constant or sequence
:
Learning rate constant or sequence
All the vectors are printed in boldface lowercase letters, and are column
vectors:
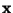 :
Observed data, an m-dimensional random vector
:
Observed data, an m-dimensional random vector
Also: the input vector of a neural network
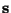 :
n-dimensional random vector of transformed components si
:
n-dimensional random vector of transformed components si
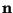 :
m-dimensional random noise vector
:
m-dimensional random noise vector
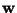 :
m-dimensional constant vector
:
m-dimensional constant vector
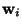 :
Weight vectors of a neural network indexed by i
:
Weight vectors of a neural network indexed by i
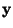 :
m-dimensional general-purpose random vector
:
m-dimensional general-purpose random vector
Also: the output vector of a neural network
All the matrices are printed in boldface capital letters:
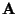 :
The constant
:
The constant 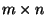 mixing matrix in the ICA model
mixing matrix in the ICA model
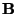 :
A transformed
:
A transformed 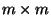 mixing matrix
mixing matrix
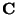 :
Covariance matrix of
:
Covariance matrix of 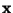 ,
,
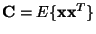
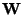 :
The weight matrix of an artificial neural network, with rows
:
The weight matrix of an artificial neural network, with rows
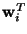
Also: A general transformation matrix
Functions:
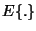 :
Mathematical expectation
:
Mathematical expectation
f(.): A probability density function
fi(.): Marginal probability density functions
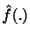 :
The characteristic function of a random variable
:
The characteristic function of a random variable
g(.): A scalar non-linear function
H(.): Differential entropy
I(.): Mutual information
J(.): Negentropy
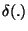 :
Kullback-Leibler divergence
:
Kullback-Leibler divergence
JG(.): Generalized contrast function
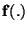 :
A general transformation from Rm to Rn
:
A general transformation from Rm to Rn
h(t): A FIR filter
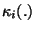 :
The i-th order cumulant of a scalar random variable
:
The i-th order cumulant of a scalar random variable
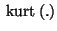 :
Kurtosis, or fourth-order cumulant
:
Kurtosis, or fourth-order cumulant
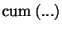 :
Cumulant (cross-cumulant) of several random variables
:
Cumulant (cross-cumulant) of several random variables
Other notation:
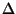 :
Change in parameter
:
Change in parameter
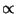 :
Proportional to (proportionality constant may change with t)
:
Proportional to (proportionality constant may change with t)
f': First derivative of function f


Next: Bibliography
Up: Survey on Independent Component
Previous: Definition of Cumulants
Aapo Hyvarinen
1999-04-23