


Next: Choosing the Contrast Function
Up: Practical choice of contrast
Previous: Practical choice of contrast
Now we shall treat the question of choosing the contrast function Gin practice.
It is useful to analyze the implications of the theoretical
results of the preceding section by considering the following
exponential power family of density functions:
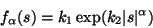 |
(11) |
where 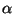 is a positive parameter, and k1,k2 are normalization
constants that ensure that
is a positive parameter, and k1,k2 are normalization
constants that ensure that
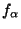 is a probability density of unit
variance. For different values of alpha, the densities in this family
exhibit different shapes. For
is a probability density of unit
variance. For different values of alpha, the densities in this family
exhibit different shapes. For
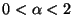 ,
one obtains a sparse,
super-Gaussian density (i.e., a density of positive kurtosis).
For
,
one obtains a sparse,
super-Gaussian density (i.e., a density of positive kurtosis).
For
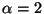 ,
one obtains the Gaussian
distribution, and for
,
one obtains the Gaussian
distribution, and for
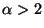 ,
a sub-Gaussian density (i.e., a density of
negative kurtosis). Thus the densities in this family can be used as
examples of different non-Gaussian densities.
,
a sub-Gaussian density (i.e., a density of
negative kurtosis). Thus the densities in this family can be used as
examples of different non-Gaussian densities.
Using Theorem 2, one sees that in terms of asymptotic
variance, an
optimal contrast function for estimating an independent component
whose density function equals
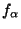 ,
is of the form:
,
is of the form:
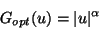 |
(12) |
where the arbitrary constants have been dropped for simplicity.
This implies roughly that
for super-Gaussian (resp. sub-Gaussian) densities, the optimal
contrast function is a function that grows slower than quadratically
(resp. faster than quadratically).
Next, recall from Section 3.1.3 that if G(u) grows fast
with |u|, the estimator becomes highly non-robust against
outliers. Taking also into account the fact that most independent
components encountered
in practice are super-Gaussian [3,25], one
reaches the conclusion
that as a general-purpose contrast function, one should choose a
function G that resembles rather
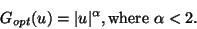 |
(13) |
The problem with such contrast functions is, however, that they are not
differentiable at 0 for
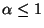 .
Thus it is better to use
approximating differentiable
functions that have the same kind of qualitative behavior. Considering
.
Thus it is better to use
approximating differentiable
functions that have the same kind of qualitative behavior. Considering
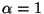 ,
in which case one has a double exponential density, one
could use instead the function
,
in which case one has a double exponential density, one
could use instead the function
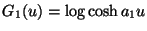 where
where 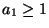 is a constant.
Note that the derivative of G1 is then the familiar tanh
function (for a1=1).
In the case of
is a constant.
Note that the derivative of G1 is then the familiar tanh
function (for a1=1).
In the case of 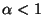 ,
i.e., highly super-Gaussian independent
components, one could
approximate the behavior of Gopt for large u
using a Gaussian function (with a minus sign):
,
i.e., highly super-Gaussian independent
components, one could
approximate the behavior of Gopt for large u
using a Gaussian function (with a minus sign):
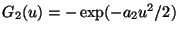 ,
where a2 is a
constant. The derivative of this function is like a sigmoid for small
values, but goes to 0 for larger values. Note that this function
also fulfills
the condition in Theorem 3, thus providing an estimator that is as
robust as possible in the framework of estimators of type (8).
As regards the constants, we have found experimentally
,
where a2 is a
constant. The derivative of this function is like a sigmoid for small
values, but goes to 0 for larger values. Note that this function
also fulfills
the condition in Theorem 3, thus providing an estimator that is as
robust as possible in the framework of estimators of type (8).
As regards the constants, we have found experimentally
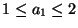 and
a2=1 to provide good
approximations.
and
a2=1 to provide good
approximations.



Next: Choosing the Contrast Function
Up: Practical choice of contrast
Previous: Practical choice of contrast
Aapo Hyvarinen
1999-04-23
![]() ,
is of the form:
,
is of the form: