

Next: Analysis of estimators and
Up: Contrast Functions for ICA
Previous: ICA data model, minimization
Contrast Functions through Approximations of Negentropy
To use the definition of ICA given above,
a simple estimate of the negentropy (or of differential entropy)
is needed.
We use here the new approximations developed in
[19], based on the maximum entropy principle. In
[19] it was shown that these
approximations are often considerably more accurate than the
conventional, cumulant-based
approximations in [7,1,26].
In the simplest case, these new approximations are of the form:
![$\displaystyle J(y_i)\approx c [E\{G(y_i)\}-E\{G(\nu)\}]^2$](img18.gif) |
|
|
(6) |
where
G is practically any non-quadratic function, c is an irrelevant
constant, and
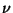 is a Gaussian variable of
zero mean and unit variance (i.e., standardized). The random variable
yi is
assumed to be of zero
mean and unit variance.
For symmetric variables, this is a generalization of the
cumulant-based approximation in
[7], which is obtained by taking
G(yi)=yi4.
The choice of the
function G is deferred to Section 3.
is a Gaussian variable of
zero mean and unit variance (i.e., standardized). The random variable
yi is
assumed to be of zero
mean and unit variance.
For symmetric variables, this is a generalization of the
cumulant-based approximation in
[7], which is obtained by taking
G(yi)=yi4.
The choice of the
function G is deferred to Section 3.
The approximation of negentropy given above in (6) gives
readily
a new objective function for estimating the ICA transform in our framework.
First, to find one independent component,
or projection pursuit direction as
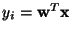 ,
we maximize the
function JG given by
,
we maximize the
function JG given by
![$\displaystyle J_G({\bf w})= [E\{G({\bf w}^T{\bf x})\}-E\{G(\nu)\}]^2$](img21.gif) |
|
|
(7) |
where 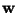 is an m-dimensional (weight) vector constrained so
that
is an m-dimensional (weight) vector constrained so
that
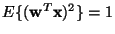 (we can fix the scale arbitrarily).
Several independent components can then be estimated one-by-one using
a deflation scheme, see Section 4.
(we can fix the scale arbitrarily).
Several independent components can then be estimated one-by-one using
a deflation scheme, see Section 4.
Second, using the approach of minimizing mutual information, the above
one-unit contrast function can be simply extended
to compute the whole matrix 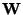 in (1).
To do this, recall from (5) that mutual information is minimized
(under the constraint of decorrelation) when the sum of the
negentropies of the components in maximized. Maximizing the sum of none-unit contrast functions, and taking into account the constraint of
decorrelation, one obtains the following
optimization problem:
in (1).
To do this, recall from (5) that mutual information is minimized
(under the constraint of decorrelation) when the sum of the
negentropies of the components in maximized. Maximizing the sum of none-unit contrast functions, and taking into account the constraint of
decorrelation, one obtains the following
optimization problem:
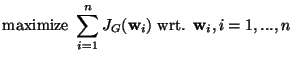 |
|
|
(8) |
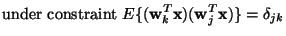 |
|
|
|
where at the maximum, every vector
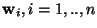 gives one of the
rows of the
matrix
gives one of the
rows of the
matrix 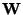 ,
and the ICA transformation is then given by
,
and the ICA transformation is then given by
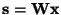 .
Thus we have defined our ICA estimator by an optimization problem.
Below we analyze the properties of the estimators, giving guidelines
for the choice of G, and propose
algorithms for solving the optimization problems in practice.
.
Thus we have defined our ICA estimator by an optimization problem.
Below we analyze the properties of the estimators, giving guidelines
for the choice of G, and propose
algorithms for solving the optimization problems in practice.


Next: Analysis of estimators and
Up: Contrast Functions for ICA
Previous: ICA data model, minimization
Aapo Hyvarinen
1999-04-23
![]() ,
we maximize the
function JG given by
,
we maximize the
function JG given by
![]() in (1).
To do this, recall from (5) that mutual information is minimized
(under the constraint of decorrelation) when the sum of the
negentropies of the components in maximized. Maximizing the sum of none-unit contrast functions, and taking into account the constraint of
decorrelation, one obtains the following
optimization problem:
in (1).
To do this, recall from (5) that mutual information is minimized
(under the constraint of decorrelation) when the sum of the
negentropies of the components in maximized. Maximizing the sum of none-unit contrast functions, and taking into account the constraint of
decorrelation, one obtains the following
optimization problem: