

Next: Properties of the FastICA
Up: The FastICA Algorithm
Previous: FastICA for several units
Finally, we give a version of FastICA that shows explicitly the
connection to the well-known infomax or maximum likelihood algorithm
introduced in [1,3,5,6].
If we express FastICA using the intermediate formula in
(42), and write it in matrix form (see [20] for details),
we see that FastICA takes the following form:
![\begin{displaymath}
{\bf W}^+={\bf W}+{\bf\Gamma}[\text{diag}(-\beta_i)+E\{g({\bf y}) {\bf y}^T\}]{\bf W}.
\end{displaymath}](img146.gif) |
(43) |
where
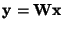 ,
,
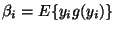 ,
and
,
and
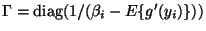 .
The matrix
.
The matrix 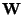 needs to be orthogonalized after every step.
In this matrix version, it is natural to orthogonalize
needs to be orthogonalized after every step.
In this matrix version, it is natural to orthogonalize 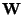 symmetrically.
symmetrically.
The above version of FastICA could be compared with the
stochastic gradient method
for maximizing likelihood [1,3,5,6]:
![\begin{displaymath}
{\bf W}^+={\bf W}+\mu[{\bf I}+g({\bf y}) {\bf y}^T]{\bf W}.
\end{displaymath}](img149.gif) |
(44) |
where 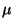 is the learning rate, not necessarily constant in time.
Comparing (46) and (47), we see that FastICA
can be considered as a fixed-point algorithm for maximum likelihood
estimation of the ICA data model. For details, see [20].
In FastICA, convergence speed is optimized by
the choice of the matrices
is the learning rate, not necessarily constant in time.
Comparing (46) and (47), we see that FastICA
can be considered as a fixed-point algorithm for maximum likelihood
estimation of the ICA data model. For details, see [20].
In FastICA, convergence speed is optimized by
the choice of the matrices
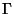 and
and
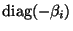 .
Another advantage of FastICA is that it can estimate both sub- and
super-gaussian independent components, which is in contrast to
ordinary ML algorithms, which only work for a given class of
distributions (see Sec. 4.4).
.
Another advantage of FastICA is that it can estimate both sub- and
super-gaussian independent components, which is in contrast to
ordinary ML algorithms, which only work for a given class of
distributions (see Sec. 4.4).


Next: Properties of the FastICA
Up: The FastICA Algorithm
Previous: FastICA for several units
Aapo Hyvarinen
2000-04-19