

Next: What is independence?
Up: Independent Component Analysis
Previous: Ambiguities of ICA
To illustrate the ICA model in statistical terms, consider two
independent components that
have the following uniform distributions:
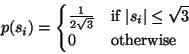 |
(5) |
The range of values for this uniform distribution were chosen so as
to make the mean zero and the variance equal to one, as was agreed in
the previous Section.
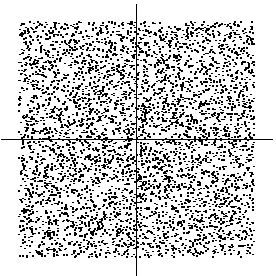
The joint density of s1 and s2 is then uniform on a square. This
follows from the basic definition that the joint density of two
independent variables is just the product of their marginal densities
(see Eq. 10): we need to simply
compute the product. The joint density is
illustrated in Figure 5 by showing data points randomly drawn
from this distribution.
Figure 5:
The joint distribution of the independent components s1and s2 with uniform distributions. Horizontal axis: s1, vertical axis: s2.
|
|
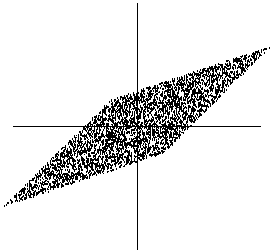
Figure 6:
The joint distribution of the observed mixtures x1 and
x2. Horizontal axis: x1, vertical axis: x2.
|
|
Now let as mix these two independent components. Let us take the
following mixing matrix:
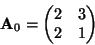 |
(6) |
This gives us two mixed variables, x1 and x2. It is easily
computed that the mixed data has a uniform distribution on a
parallelogram, as shown in Figure 6. Note that the
random variables x1 and x2 are not independent any more; an easy
way to see this is to consider, whether it is possible to predict the
value of one of them, say x2, from the value of the other. Clearly
if x1 attains one of its maximum or minimum values, then this completely
determines the value of x2. They are therefore not
independent. (For variables s1 and s2 the situation is
different: from Fig. 5 it can be seen that knowing the
value of s1 does not in any way help in guessing the value of
s2.)
The problem of estimating the data model of ICA is now to estimate the
mixing matrix 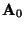 using only information contained in the mixtures
x1 and x2. Actually, you can see from Figure 6
an intuitive way of estimating
using only information contained in the mixtures
x1 and x2. Actually, you can see from Figure 6
an intuitive way of estimating  :
The edges of the parallelogram
are in the directions of the columns of
:
The edges of the parallelogram
are in the directions of the columns of  .
This means that we could,
in principle, estimate the ICA model by first estimating the joint
density of x1 and x2, and then locating the edges. So, the
problem seems to have a solution.
.
This means that we could,
in principle, estimate the ICA model by first estimating the joint
density of x1 and x2, and then locating the edges. So, the
problem seems to have a solution.
In reality, however,
this would be a very poor method because it only works with variables
that have exactly uniform distributions. Moreover, it would be
computationally quite complicated. What we need is a method that
works for any distributions of the independent components, and works
fast and reliably.
Next we shall consider the exact definition of independence before
starting to develop methods for estimation of the ICA model.


Next: What is independence?
Up: Independent Component Analysis
Previous: Ambiguities of ICA
Aapo Hyvarinen
2000-04-19
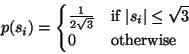
![]() using only information contained in the mixtures
x1 and x2. Actually, you can see from Figure 6
an intuitive way of estimating
using only information contained in the mixtures
x1 and x2. Actually, you can see from Figure 6
an intuitive way of estimating ![]() :
The edges of the parallelogram
are in the directions of the columns of
:
The edges of the parallelogram
are in the directions of the columns of ![]() .
This means that we could,
in principle, estimate the ICA model by first estimating the joint
density of x1 and x2, and then locating the edges. So, the
problem seems to have a solution.
.
This means that we could,
in principle, estimate the ICA model by first estimating the joint
density of x1 and x2, and then locating the edges. So, the
problem seems to have a solution.