


Next: Other applications
Up: Applications of ICA
Previous: Feature extraction
A less direct application of the ICA methods can be found in blind
deconvolution (see Section 2).
Due to the fact that the values of the original signal s(t) are
independent for different t, this problem can be solved using
essentially the
same formalism as used in ICA, as noted above. Indeed this problem can
also be represented (though only approximately)
by Eq. (11);
then the realizations of
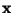 and
and 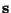 are vectors containing n=m subsequent observations of
the signals x(t) and s(t), beginning at different points of time.
In other words, a sequence of observations
are vectors containing n=m subsequent observations of
the signals x(t) and s(t), beginning at different points of time.
In other words, a sequence of observations
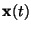 is such that
is such that
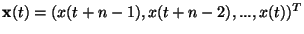 for
for
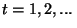 .
The square matrix
.
The square matrix  is determined by
the convolving filter. Though this formulation is only approximative,
the exact formulation using linear filters would lead to essentially the
same algorithms and convergence proofs. Also blind separation of
several convolved signals ('multi-channel deconvolution') can be
represented combining these two
approaches, see, for example, [41,123,137,149,150,134,92].
is determined by
the convolving filter. Though this formulation is only approximative,
the exact formulation using linear filters would lead to essentially the
same algorithms and convergence proofs. Also blind separation of
several convolved signals ('multi-channel deconvolution') can be
represented combining these two
approaches, see, for example, [41,123,137,149,150,134,92].
Aapo Hyvarinen
1999-04-23