


Next: Non-linear decorrelation algorithms
Up: Algorithms for ICA
Previous: Preprocessing of the data
The pioneering work in [80] was
inspired by neural
networks. Their algorithm was based on canceling the
non-linear cross-correlations, see Section 4.3.3.
The non-diagonal terms of the matrix 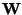 are updated according
to
are updated according
to
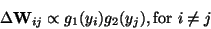 |
(33) |
where g1 and g2 are some odd non-linear functions, and the yiare computed at every iteration as
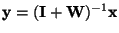 .
The
diagonal terms
.
The
diagonal terms
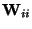 are set to zero. The yi then give, after
convergence, estimates of the independent components.
Unfortunately, the algorithm converges only under
rather severe restrictions (see [40]).
are set to zero. The yi then give, after
convergence, estimates of the independent components.
Unfortunately, the algorithm converges only under
rather severe restrictions (see [40]).
Aapo Hyvarinen
1999-04-23