

Next: Algorithms for maximum likelihood
Up: Algorithms for ICA
Previous: Jutten-Hérault algorithm
Further algorithms for canceling non-linear cross-correlations were
introduced independently in
[34,33,30] and [91,28].
Compared to the Jutten-Hérault algorithm, these algorithms reduce
the computational overhead by avoiding any matrix
inversions, and improve its stability. For example, the following
algorithm was given in [34,33]:
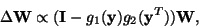 |
(34) |
where
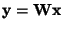 ,
the
non-linearities g1(.) and g2(.) are applied separately on every
component of the vector
,
the
non-linearities g1(.) and g2(.) are applied separately on every
component of the vector 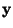 ,
and the
identity matrix could be replaced by any positive definite diagonal matrix.
In [91,28], the following algorithm called the EASI
algorithm was introduced:
,
and the
identity matrix could be replaced by any positive definite diagonal matrix.
In [91,28], the following algorithm called the EASI
algorithm was introduced:
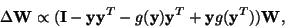 |
(35) |
A principled way of choosing the non-linearities used in these learning
rules is provided by the maximum likelihood (or infomax) approach
as described in the next subsection.
Aapo Hyvarinen
1999-04-23