

Next: Contrast Functions through Approximations
Up: Contrast Functions for ICA
Previous: Contrast Functions for ICA
One popular way of formulating the ICA problem is to consider the
estimation of the following generative model for the data
[1,3,5,6,23,24,27,28,31]:
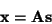 |
(2) |
where 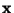 is an observed m-dimensional vector,
is an observed m-dimensional vector, 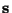 is an
n-dimensional (latent) random vector whose components are assumed mutually
independent, and
is an
n-dimensional (latent) random vector whose components are assumed mutually
independent, and 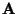 is a constant
is a constant 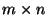 matrix to be estimated.
It is usually further assumed
that the dimensions of
matrix to be estimated.
It is usually further assumed
that the dimensions of 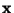 and
and 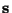 are equal, i.e., m=n; we make
this assumption in the rest of the paper.
A noise vector may also be present. The matrix
are equal, i.e., m=n; we make
this assumption in the rest of the paper.
A noise vector may also be present. The matrix
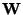 defining the transformation as in (1) is then
obtained as the (pseudo)inverse of the estimate of the matrix
defining the transformation as in (1) is then
obtained as the (pseudo)inverse of the estimate of the matrix 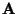 .
Non-Gaussianity of the independent components is necessary
for the identifiability of the model (2), see [7].
.
Non-Gaussianity of the independent components is necessary
for the identifiability of the model (2), see [7].
Comon [7] showed how to obtain a more general formulation
for ICA that does not need to assume an underlying data model.
This definition is based on the concept of mutual information.
First, we define the differential entropy Hof a random vector
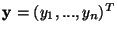 with density f(.) as follows
[33]:
with density f(.) as follows
[33]:
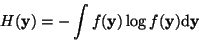 |
(3) |
Differential entropy can be normalized to give rise to the definition of
negentropy, which has the appealing property of being invariant for linear
transformations. The definition of negentropy J is given by
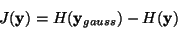 |
(4) |
where
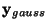 is a Gaussian random vector of the same covariance matrix
as
is a Gaussian random vector of the same covariance matrix
as 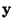 .
Negentropy can also be interpreted as a measure of
nongaussianity [7].
Using the concept of differential entropy, one can define
the mutual information I between the n (scalar) random variables
yi,
i=1...n[8,7].
Mutual information is a natural measure of the dependence between
random variables.
It is particularly interesting to express mutual information using
negentropy, constraining the variables to be uncorrelated. In
this case, we have [7]
.
Negentropy can also be interpreted as a measure of
nongaussianity [7].
Using the concept of differential entropy, one can define
the mutual information I between the n (scalar) random variables
yi,
i=1...n[8,7].
Mutual information is a natural measure of the dependence between
random variables.
It is particularly interesting to express mutual information using
negentropy, constraining the variables to be uncorrelated. In
this case, we have [7]
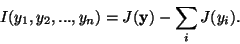 |
(5) |
Since mutual information is the information-theoretic
measure of the independence of random variables, it is natural to use it
as the criterion for finding the ICA transform. Thus we define in this
paper, following [7], the ICA
of a random vector 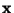 as an invertible transformation
as an invertible transformation
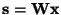 as in
(1) where the matrix
as in
(1) where the matrix 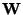 is determined so that the mutual information of the transformed components si is minimized.
Note that mutual information (or the independence of
the components) is not affected by
multiplication of the components by scalar constants. Therefore, this
definition only defines the independent components up to some
multiplicative constants.
Moreover, the constraint of uncorrelatedness of
the si is adopted in this paper.
This constraint is not strictly necessary, but
simplifies the computations considerably.
is determined so that the mutual information of the transformed components si is minimized.
Note that mutual information (or the independence of
the components) is not affected by
multiplication of the components by scalar constants. Therefore, this
definition only defines the independent components up to some
multiplicative constants.
Moreover, the constraint of uncorrelatedness of
the si is adopted in this paper.
This constraint is not strictly necessary, but
simplifies the computations considerably.
Because negentropy is invariant for invertible linear transformations
[7], it is now
obvious from (5) that finding an invertible transformation 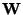 that
minimizes the mutual information is roughly equivalent to finding
directions in which the negentropy is maximized.
This formulation of ICA also shows explicitly the
connection between ICA and projection pursuit
[11,12,16,26].
In fact, finding a single direction that maximizes negentropy
is a form of projection pursuit, and could also be interpreted as
estimation of a single independent component [24].
that
minimizes the mutual information is roughly equivalent to finding
directions in which the negentropy is maximized.
This formulation of ICA also shows explicitly the
connection between ICA and projection pursuit
[11,12,16,26].
In fact, finding a single direction that maximizes negentropy
is a form of projection pursuit, and could also be interpreted as
estimation of a single independent component [24].


Next: Contrast Functions through Approximations
Up: Contrast Functions for ICA
Previous: Contrast Functions for ICA
Aapo Hyvarinen
1999-04-23
![]() with density f(.) as follows
[33]:
with density f(.) as follows
[33]:
![]() as an invertible transformation
as an invertible transformation
![]() as in
(1) where the matrix
as in
(1) where the matrix ![]() is determined so that the mutual information of the transformed components si is minimized.
Note that mutual information (or the independence of
the components) is not affected by
multiplication of the components by scalar constants. Therefore, this
definition only defines the independent components up to some
multiplicative constants.
Moreover, the constraint of uncorrelatedness of
the si is adopted in this paper.
This constraint is not strictly necessary, but
simplifies the computations considerably.
is determined so that the mutual information of the transformed components si is minimized.
Note that mutual information (or the independence of
the components) is not affected by
multiplication of the components by scalar constants. Therefore, this
definition only defines the independent components up to some
multiplicative constants.
Moreover, the constraint of uncorrelatedness of
the si is adopted in this paper.
This constraint is not strictly necessary, but
simplifies the computations considerably.
![]() that
minimizes the mutual information is roughly equivalent to finding
directions in which the negentropy is maximized.
This formulation of ICA also shows explicitly the
connection between ICA and projection pursuit
[11,12,16,26].
In fact, finding a single direction that maximizes negentropy
is a form of projection pursuit, and could also be interpreted as
estimation of a single independent component [24].
that
minimizes the mutual information is roughly equivalent to finding
directions in which the negentropy is maximized.
This formulation of ICA also shows explicitly the
connection between ICA and projection pursuit
[11,12,16,26].
In fact, finding a single direction that maximizes negentropy
is a form of projection pursuit, and could also be interpreted as
estimation of a single independent component [24].