Consistency

First of all, we prove that $\hat{{\bf w}}$ is a (locally) consistent estimator for one component in the ICA data model. To prove this, we have the following theorem:

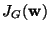
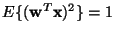
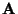
Theorem 1   Assume that the input data follows the ICA data model in (2), and that G is a sufficiently smooth even function. Then the set of local maxima of $J_G({\bf w})$ under the constraint $E\{({\bf w}^T{\bf x})^2\}=1$, includes the i-th row of the inverse of the mixing matrix ${\bf A}$such that the corresponding independent component s_i fulfills

$$E\{s_i g(s_i) - g'(s_i)\} [E\{G(s_i)\} - E\{G( \nu)\}] > 0$$ (9)

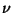
where g(.) is the derivative of G(.), and $\nu$ is a standardized Gaussian variable.

This theorem can be considered a corollary of the theorem in [24]. The condition in Theorem 1 seems to be true for most reasonable choices of G, and distributions of the s_i. In particular, if G(u)=u⁴, the condition is fulfilled for any distribution of non-zero kurtosis. In that case, it can also be proven that there are no spurious optima [9].