

Next: Connection to mutual information
Up: Maximum Likelihood Estimation
Previous: The likelihood
Another related contrast function was derived from a neural network
viewpoint in [3,35]. This was based on maximizing the
output entropy (or information flow) of a neural network with
non-linear outputs. Assume
that 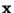 is the input to the neural network whose outputs are of the
form
is the input to the neural network whose outputs are of the
form
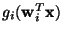 ,
where the gi are some non-linear scalar functions, and the
,
where the gi are some non-linear scalar functions, and the 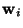 are the weight vectors of the neurons.
One then wants to maximize the entropy of the outputs:
are the weight vectors of the neurons.
One then wants to maximize the entropy of the outputs:
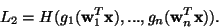 |
(28) |
If the gi are well chosen, this framework also enables the
estimation of the ICA model.
Indeed,
several authors, e.g., [4,37], proved the
surprising result that the principle of network entropy maximization,
or ``infomax'', is equivalent to
maximum likelihood estimation. This
equivalence requires that the non-linearities gi used in the
neural network are chosen as the cumulative distribution functions
corresponding to the densities fi, i.e.,
gi'(.)=fi(.).
Aapo Hyvarinen
2000-04-19
![]() is the input to the neural network whose outputs are of the
form
is the input to the neural network whose outputs are of the
form
![]() ,
where the gi are some non-linear scalar functions, and the
,
where the gi are some non-linear scalar functions, and the ![]() are the weight vectors of the neurons.
One then wants to maximize the entropy of the outputs:
are the weight vectors of the neurons.
One then wants to maximize the entropy of the outputs: