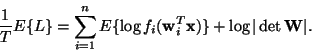Connection to mutual information

To see the connection between likelihood and mutual information, consider the expectation of the log-likelihood:

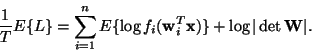$$\frac{1}{T}E\{L\}=\sum_{i=1}^n E\{\log f_i({\bf w}_i^T {\bf x})\}+\log\vert\det {\bf W}\vert.$$ (29)

Actually, if the f_i were equal to the actual distributions of ${\bf w}_i^T{\bf x}$, the first term would be equal to $- \sum_i H({\bf w}_i^T{\bf x})$. Thus the likelihood would be equal, up to an additive constant, to the negative of mutual information as given in Eq. (28).

Actually, in practice the connection is even stronger. This is because in practice we don't know the distributions of the independent components. A reasonable approach would be to estimate the density of ${\bf w}_i^T{\bf x}$ as part of the ML estimation method, and use this as an approximation of the density of s_i. In this case, likelihood and mutual information are, for all practical purposes, equivalent.

Nevertheless, there is a small difference that may be very important in practice. The problem with maximum likelihood estimation is that the densities f_i must be estimated correctly. They need not be estimated with any great precision: in fact it is enough to estimate whether they are sub- or supergaussian [5,25,31]. In many cases, in fact, we have enough prior knowledge on the independent components, and we don't need to estimate their nature from the data. In any case, if the information on the nature of the independent components is not correct, ML estimation will give completely wrong results. Some care must be taken with ML estimation, therefore. In contrast, using reasonable measures of nongaussianity, this problem does not usually arise.