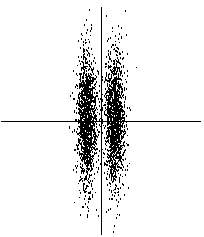ICA and Projection Pursuit

It is interesting to note how our approach to ICA makes explicit the connection between ICA and projection pursuit. Projection pursuit [12,13,16,27] is a technique developed in statistics for finding ``interesting'' projections of multidimensional data. Such projections can then be used for optimal visualization of the data, and for such purposes as density estimation and regression. In basic (1-D) projection pursuit, we try to find directions such that the projections of the data in those directions have interesting distributions, i.e., display some structure. It has been argued by Huber [16] and by Jones and Sibson [27] that the Gaussian distribution is the least interesting one, and that the most interesting directions are those that show the least Gaussian distribution. This is exactly what we do to estimate the ICA model.

The usefulness of finding such projections can be seen in Fig. 9, where the projection on the projection pursuit direction, which is horizontal, clearly shows the clustered structure of the data. The projection on the first principal component (vertical), on the other hand, fails to show this structure.

  

Figure 9: An illustration of projection pursuit and the ``interestingness'' of nongaussian projections. The data in this figure is clearly divided into two clusters. However, the principal component, i.e. the direction of maximum variance, would be vertical, providing no separation between the clusters. In contrast, the strongly nongaussian projection pursuit direction is horizontal, providing optimal separation of the clusters.

Thus, in the general formulation, ICA can be considered a variant of projection pursuit. All the nongaussianity measures and the corresponding ICA algorithms presented here could also be called projection pursuit ``indices'' and algorithms. In particular, the projection pursuit allows us to tackle the situation where there are less independent components s_i than original variables x_i is. Assuming that those dimensions of the space that are not spanned by the independent components are filled by gaussian noise, we see that computing the nongaussian projection pursuit directions, we effectively estimate the independent components. When all the nongaussian directions have been found, all the independent components have been estimated. Such a procedure can be interpreted as a hybrid of projection pursuit and ICA.

However, it should be noted that in the formulation of projection pursuit, no data model or assumption about independent components is made. If the ICA model holds, optimizing the ICA nongaussianity measures produce independent components; if the model does not hold, then what we get are the projection pursuit directions.