It is a tempting alternative to try ICA on financial data. There are many situations in that application domain in which parallel time series are available, such as currency exchange rates or daily returns of stocks, that may have some common underlying factors. ICA might reveal some driving mechanisms that otherwise remain hidden. In a recent study of a stock portfolio [2], it was found that ICA is a complementary tool to PCA, allowing the underlying structure of the data to be more readily observed.
In [30], we applied ICA on a different problem: the cashflow of several stores belonging to the same retail chain, trying to find the fundamental factors common to all stores that affect the cashflow data. Thus, the cashflow effect of the factors specific to any particular store, i.e., the effect of the actions taken at the individual stores and in its local environment could be analyzed.
The assumption of having some underlying independent components in this specific application may not be unrealistic. For example, factors like seasonal variations due to holidays and annual variations, and factors having a sudden effect on the purchasing power of the customers like prize changes of various commodities, can be expected to have an effect on all the retail stores, and such factors can be assumed to be roughly independent of each other. Yet, depending on the policy and skills of the individual manager like e.g. advertising efforts, the effect of the factors on the cash flow of specific retail outlets are slightly different. By ICA, it is possible to isolate both the underlying factors and the effect weights, thus also making it possible to group the stores on the basis of their managerial policies using only the cash flow time series data.
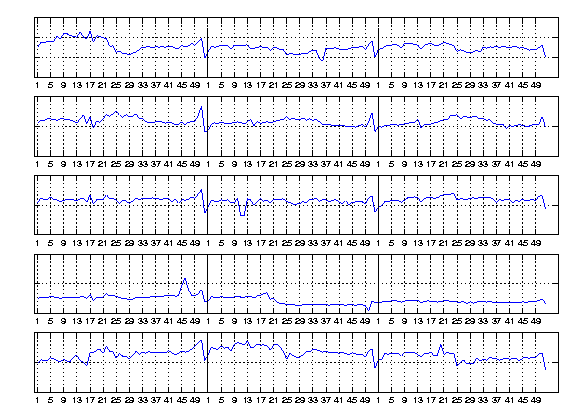
The data consisted of the weekly cash flow in 40 stores that belong to the same retail chain; the cash flow measurements cover 140 weeks. Some examples of the original data xi(t) are shown in Fig. 13.
|
The prewhitening was performed so that the original signal vectors
were projected to the subspace spanned by their first five principal
components and the variances were normalized to 1. Thus the dimension
of the signal space was decreased from 40 to 5. Using the FastICA
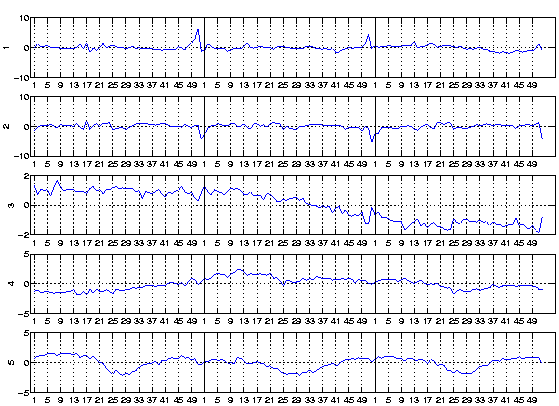
algorithm, four IC's
were estimated. As
depicted in Fig. 14, the FastICA algorithm has found
several clearly different fundamental factors hidden in the original
data.
The factors have clearly different interpretations. The upmost two factors follow the sudden changes that are caused by holidays etc.; the most prominent example is the Christmas time. The factor on the bottom row, on the other hand, reflects the slower seasonal variation, with the effect of the summer holidays clearly visible. The factor on the third row could represent a still slower variation, something resembling a trend. The last factor, on the fourth row, is different from the others; it might be that this factor follows mostly the relative competitive position of the retail chain with respect to its competitors, but other interpretations are also possible.
|
More details on the experiments and their interpretation can be found in [30].