Statistical independence

To begin with, we shall recall some basic definitions needed. Denote by y₁,y₂,...,y_m some random variables with joint density f(y₁,...,y_m). For simplicity, assume that the variables are zero-mean. The variables y_i are (mutually) independent, if the density function can be factorized [122]:

 

f(y₁,...,y_m)=f₁(y₁)f₂(y₂)...f_m(y_m) (7)

where f_i(y_i) denotes the marginal density of y_i. To distinguish this form of independence from other concepts of independence, for example, linear independence, this property is sometimes called statistical independence.

Independence must be distinguished from uncorrelatedness, which means that

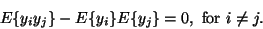$$E\{y_i y_j\}-E\{y_i\}E\{y_j\}=0, \mbox{ for }i\neq j.$$ (8)

Independence is in general a much stronger requirement than uncorrelatedness. Indeed, if the y_i are independent, one has

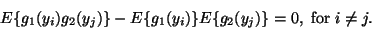$$E\{g_1(y_i) g_2(y_j)\}-E\{g_1(y_i)\}E\{ g_2(y_j)\}=0, \mbox{ for }i\neq j.$$ (9)

for any² functions g₁ and g₂ [122]. This is clearly a stricter condition than the condition of uncorrelatedness. There is, however, an important special case where independence and uncorrelatedness are equivalent. This is the case when y₁,...,y_m have a joint Gaussian distribution (see [36]). Due to this property, independent component analysis is not interesting (or possible) for Gaussian variables, as will be seen below.