- ... deconvolution1
- Often the term 'blind equalization' is
used in the same sense.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... any2
- The functions must be assumed measurable. We shall,
however, omit any questions of measurability in this paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... voices3
- This application is to be taken rather
as an illustrative example than a real application. In practice, the
situation is much more complicated than described here due to echos
and, above all, time delays, see Section 7.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...[50,56]4
- Note that it is
possible, at least in theory, to
consider the robustness of estimators even in the case of the
ICA model without any noise. This is because the
distribution of
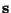 may be
may be 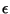 -contaminated, or contain
outliers, even if
-contaminated, or contain
outliers, even if 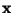 were generated from
were generated from 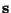 exactly according to
the noise-free model. A more realistic analysis of robustness would
require, however, the introduction of noise in the model.
exactly according to
the noise-free model. A more realistic analysis of robustness would
require, however, the introduction of noise in the model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
optimal5
- Here we consider robustness to be one form of
optimality, in particular, minimax-optimality in the neighborhood of
the assumed model in a space of statistical models [56].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.