Relations to classical methods

ICA is closely related to several of the methods described in Section 2.

1.

By definition, ICA can be considered a method for achieving redundancy reduction. Indeed, there is experimental evidence that for certain kinds of sensory data, the conventional ICA algorithms do find directions that are compatible with existing neurophysiological data, assumed to reflect redundancy reduction [14,58,116]. See Section 3.5.2.

2.

In the noise-free case, the estimation of the ICA model means simply finding certain 'interesting' projections, which give estimates of the independent components. Thus ICA can be considered, at least using Definitions 1 and 3, a special case of projection pursuit. Indeed, as will be explained in Section 4, the conventional criteria used for finding the 'interesting' directions in projections pursuit coincide essentially with the criteria used for estimating the independent components.

3.

Another close affinity can be found between ICA and blind deconvolution (more precisely, the special case of blind deconvolution where the original signal is i.i.d. over time). Due to the assumption that the values of the original signal s(t) are independent for different t, this problem is formally closely related to the problem of independent component analysis. Indeed, many ideas developed for blind deconvolution can be directly applied for ICA, and vice versa. Blind deconvolution, and especially the elegant and powerful framework developed in [42], can thus be considered an intellectual ancestor of ICA.

4.

Comparing Eq. (10) in Definition 2 with the definition of factor analysis in Eq. (5), the connection between factor analysis and ICA becomes clear. Indeed, ICA may be considered a non-Gaussian factor analysis. The main difference is that usually in ICA, reduction of dimension is considered only as a secondary objective, but this need not be the case. Indeed, a simple combination of factor analysis and ICA can be obtained using factor rotations. Above we saw that after finding the factor subspace, a suitable rotation is usually performed. ICA could also be conceived as such a rotation, where the criterion depends on the higher-order statistics of the factors, instead of the structure of the matrix 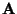${\bf A}$. Such a method is roughly equivalent to the method advocated in [71,61,84], which consists of first reducing the dimension by PCA, and then performing ICA without further dimension reduction.

5.

Using Definition 1, the relation to principal component analysis is also evident. Both methods formulate a general objective function that define the 'interestingness' of a linear representation, and then maximize that function. A second relation between PCA and ICA is that both are related to factor analysis, though under the contradictory assumptions of Gaussianity and non-Gaussianity, respectively. The affinity between PCA and ICA may be, however, less important than the affinity between ICA and the other methods discussed above. This is because PCA and ICA define their objective functions in quite different ways. PCA uses only second-order statistics, while ICA is impossible using only second-order statistics. PCA emphasizes dimension reduction, while ICA may reduce the dimension, increase it or leave it unchanged. However, the relation between ICA and nonlinear versions of the PCA criteria, as defined in [82,112], is quite strong, as will be seen in the next Section.

The connections between ICA and some other methods are illustrated in Fig. 4. The lines in the diagram indicate very close connections, under the assumptions given next to the lines. First, if no assumptions on the data are made, and in particular no noise is postulated in the data, ICA can be considered a method of exploratory data analysis, as projection pursuit. Indeed, using Definition 1, ICA means simply finding some interesting projections of the data, and the measures of interestingness are essentially equivalent in the two methods, as will be seen in the next Section. On the other hand, if one assumes a noisy data model, as in Definition 2, ICA can be considered a variation of factor analysis for non-Gaussian data. Thus one has two possible approaches to ICA that are quite different as they stem from two clearly distinct classical methods. ICA according to Definition 3, or the noise-free ICA data model, is something between these two approaches. As for PCA, its connection to ICA can be considered indirect, since it can be used to perform factor analysis for Gaussian data.

  

Figure 4: The relations between ICA and some other methods. The lines show close connections, and the texts next to the lines show the assumptions needed for the connection.