Blind source separation

The classical application of the ICA model is blind source separation [80]. In blind source separation, the observed values of ${\bf x}$ correspond to a realization of an m-dimensional discrete-time signal ${\bf x}(t)$, t=1,2,.... Then the independent components s_i(t) are called source signals, which are usually original, uncorrupted signals or noise sources. A classical example of blind source separation is the cocktail party problem. Assume that several people are speaking simultaneously in the same room, as in a cocktail party. Then the problem is to separate the voices of the different speakers, using recordings of several microphones in the room. In principle, this corresponds to the ICA data model, where x_i(t)is the recording of the i-th microphone, and the s_i(t) are the waveforms of the voices³. A more practical application is noise reduction. If one of the sources is the original, uncorrupted source and the others are noise sources, estimation of the uncorrupted source is in fact a denoising operation.

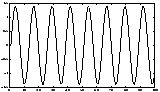
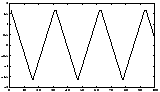
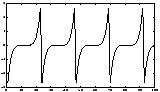
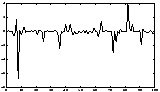
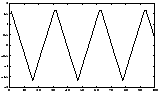
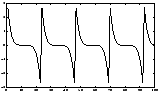
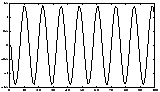
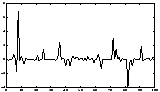
A simple artificial illustration of blind source separation is given in Figures 5-7. In this illustration, deterministic signals were used for purposes of illustration. However, the spectral properties of the signals are not used in the ICA framework, and thus the results would remain unchanged if the signals were simply (non-Gaussian) white noise.

  

Figure 5: An illustration of blind source separation. This figure shows four source signals, or independent components.

  

Figure 6: Due to some external circumstances, only linear mixtures of the source signals in Fig. 5, as depicted here, can be observed.

  

Figure 7: Using only the linear mixtures in Fig. 6, the source signals in Fig. 5 can be estimated, up to some multiplying factors. This figure shows the estimates of the source signals.

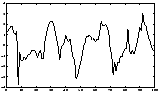
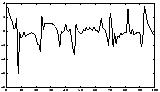
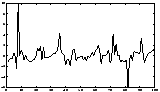
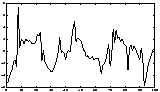In [140,141,101], results on applying ICA for blind separation of electroencephalographic (EEG) and magnetoencephalographic (MEG) data were reported. The EEG data consisted of recordings of brain activity obtained using electrodes attached to the scalp. Thus a 23-dimensional signal vector was observed. The MEG data was obtained with a more sophisticated measuring method, giving rise to a 122-dimensional signal vector. The ICA algorithms succeeded in separating certain source signals that were so-called artifacts, or noise sources not corresponding to brain activity [140,141]. Canceling these noise sources is a central, and as yet unsolved problem in EEG and MEG signal processing. ICA offers a very promising method. Similarly, ICA can be used for decomposition of evoked field potentials measured by EEG or MEG [142,143], which is an application of considerable interest in the neurosciences. Application on further brain imaging data, this time obtained by functional magnetic resonance imaging (fMRI), is reported in [104].

Another application area is on economic time series. Some work is reported in [89]. Very recently, applications on telecommunications have also been published [125].

Since most of the research on ICA has been done with the application of source separation in mind, many authors treating the ICA problem do not use the term ICA, but speak simply of blind source separation (BSS). We make, however, a clear distinction between ICA, which is a theoretical problem or data model with different applications, and blind source separation, which is an application that can be solved using various theoretical approaches, including but not limited to ICA. In fact, the blind source separation problem can be solved using methods very different from ICA. In particular, methods using frequency information, or spectral properties, are prominent (see [16,18,136,147,135,105]). These methods can be used for time-correlated signals, which is of course the usual case in blind source separation, but not in many other applications of ICA (see below). Using such frequency methods, it is also possible to separate Gaussian source signals.