One-unit contrast functions

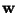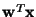We use the expression 'one-unit contrast function' to designate any function whose optimization enables estimation of a single independent component. Thus, instead of estimating the whole ICA model, we try to find here simply one vector, say ${\bf w}$, so that the linear combination ${\bf w}^T{\bf x}$ equals one of the independent components s_i. This procedure can be iterated to find several independent components. The use of one-unit contrast functions can be motivated by the following:

• The one-unit approach shows a direct connection to projection pursuit. Indeed, all the one-unit contrast functions discussed below can be considered as measures of non-Gaussianity, and therefore this approach gives a unifying framework for these two techniques. The same contrast functions and algorithms can be interpreted in two different ways.
• In many applications, one does not need to estimate all the independent components. Finding only some of them is enough. In the ideal case where the one-unit contrast functions are optimized globally, the independent components are obtained in the order of (descending) non-Gaussianity. In the light of the basic principles of projection pursuit, this means that the most interesting independent components are obtained first. This reduces the computational complexity of the method considerably, if the input data has a high dimension.
• Prior knowledge of the number of independent components is not needed, since the independent components can be estimated one-by-one.
• This approach also shows clearly the connection to neural networks. One can construct a neural network whose units learn so that every neuron optimizes its own contrast function. Thus the approach tends to lead to computationally simple solutions.

After estimating one independent component, one can use simple decorrelation to find a different independent component, since the independent components are by definition uncorrelated. Thus, maximizing the one-unit contrast function under the constraint of decorrelation (with respect to the independent components already found), a new independent component can be found, and this procedure can be iterated to find all the independent components. Symmetric (parallel) decorrelation can also be used, see [71,60,65,84].