


Next: Higher-order cumulants
Up: One-unit contrast functions
Previous: One-unit contrast functions
Negentropy
A most natural information-theoretic one-unit contrast function is negentropy.
From Eq. (15), one is tempted to conclude that the
independent components correspond to directions in which the
differential entropy of
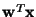 is minimized. This turns out to be
roughly the case. However, a modification has to be made, since
differential entropy is not invariant for scale transformations.
To obtain a linearly (and, in fact, affinely) invariant version
of entropy, one defines the negentropy J as follows
is minimized. This turns out to be
roughly the case. However, a modification has to be made, since
differential entropy is not invariant for scale transformations.
To obtain a linearly (and, in fact, affinely) invariant version
of entropy, one defines the negentropy J as follows
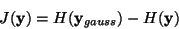 |
(22) |
where
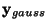 is a Gaussian random vector of the same covariance matrix
as
is a Gaussian random vector of the same covariance matrix
as 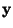 .
Negentropy, or negative normalized entropy, is always non-negative,
and is zero if and only if
.
Negentropy, or negative normalized entropy, is always non-negative,
and is zero if and only if 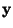 has a Gaussian distribution
[36].
has a Gaussian distribution
[36].
The usefulness of this definition can be seen when mutual information
is expressed using negentropy, giving
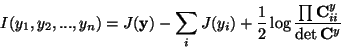 |
(23) |
where 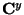 is the covariance matrix of
is the covariance matrix of 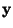 ,
and the
,
and the
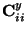 are its diagonal elements.
If the yi are uncorrelated, the third term is 0, and we thus obtain
are its diagonal elements.
If the yi are uncorrelated, the third term is 0, and we thus obtain
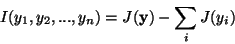 |
(24) |
Because negentropy is invariant for linear transformations
[36], it is now
obvious that finding maximum negentropy directions, i.e., directions
where the elements of the sum J(yi)are maximized, is equivalent to finding a representation
in which mutual information is minimized.
The use of negentropy shows clearly the connection between ICA and
projection pursuit. Using differential entropy as a projection
pursuit index, as has been suggested in [57,78],
amounts to finding directions in which
negentropy is maximized.
Unfortunately, the reservations made with respect to mutual
information are also valid here. The estimation of negentropy is
difficult, and therefore this contrast function remains mainly a
theoretical one. As in the multi-unit case, negentropy can be
approximated by higher-order cumulants, for example as follows [78]:
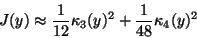 |
(25) |
where
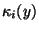 is the i-th order cumulant of y.
The random variable y is assumed to be of zero mean and unit variance.
However, the validity of such
approximations may be rather limited.
In [64], it was argued that cumulant-based approximations
of negentropy are inaccurate, and in many cases too sensitive to
outliers. New approximations of negentropy were therefore introduced.
In the simplest case, these new approximations are of the form:
is the i-th order cumulant of y.
The random variable y is assumed to be of zero mean and unit variance.
However, the validity of such
approximations may be rather limited.
In [64], it was argued that cumulant-based approximations
of negentropy are inaccurate, and in many cases too sensitive to
outliers. New approximations of negentropy were therefore introduced.
In the simplest case, these new approximations are of the form:
![$\displaystyle J(y)\approx c [E\{G(y)\}-E\{G(\nu)\}]^2$](img89.gif) |
|
|
(26) |
where
G is practically any non-quadratic function, c is an irrelevant
constant, and
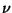 is a Gaussian variable of
zero mean and unit variance (i.e., standardized).
For the practical choice of G, see below.
In [64], these approximations were shown to be better
than the cumulant-based ones in several respects.
is a Gaussian variable of
zero mean and unit variance (i.e., standardized).
For the practical choice of G, see below.
In [64], these approximations were shown to be better
than the cumulant-based ones in several respects.
Actually, the two approximations of negentropy discussed above are
interesting as one-unit contrast functions in their own right, as will
be discussed next.



Next: Higher-order cumulants
Up: One-unit contrast functions
Previous: One-unit contrast functions
Aapo Hyvarinen
1999-04-23
![]() is minimized. This turns out to be
roughly the case. However, a modification has to be made, since
differential entropy is not invariant for scale transformations.
To obtain a linearly (and, in fact, affinely) invariant version
of entropy, one defines the negentropy J as follows
is minimized. This turns out to be
roughly the case. However, a modification has to be made, since
differential entropy is not invariant for scale transformations.
To obtain a linearly (and, in fact, affinely) invariant version
of entropy, one defines the negentropy J as follows