


Next: Non-linear PCA algorithms
Up: Algorithms for ICA
Previous: Non-linear decorrelation algorithms
An important class of algorithms consists of those based on
maximization of network entropy (infomax) [12], which is, under some
conditions, equivalent to
the maximum likelihood approach [124] (see
Section 4.3.1). Usually these algorithms are based on
(stochastic) gradient ascent of the objective function. For example, the
following algorithm was derived in [12]:
![\begin{displaymath}
\Delta {\bf W}\propto [{\bf W}^T]^{-1}-2\mbox{tanh}({\bf W}{\bf x}){\bf x}^T
\end{displaymath}](img124.gif) |
(36) |
where the tanh function is applied separately on every component of the
vector
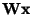 ,
as above. The tanh function is used here because it is the
derivative of the log-density of the 'logistic' distribution
[12]. This function works for
estimation of most super-Gaussian (sparse) independent components; for
sub-Gaussian independent components, other functions must be used, see
e.g. [124,26,96].
The algorithm in Eq. (36) converges, however, very slowly, as
has been noted by several researchers. The
convergence may be improved by whitening the data, and especially
by using the natural gradient.
,
as above. The tanh function is used here because it is the
derivative of the log-density of the 'logistic' distribution
[12]. This function works for
estimation of most super-Gaussian (sparse) independent components; for
sub-Gaussian independent components, other functions must be used, see
e.g. [124,26,96].
The algorithm in Eq. (36) converges, however, very slowly, as
has been noted by several researchers. The
convergence may be improved by whitening the data, and especially
by using the natural gradient.
The natural (or relative) gradient method
simplifies the gradient method considerably, and makes it better conditioned.
The principle of the natural gradient [1,2] is based on
the geometrical
structure of the parameter space, and is related to the
principle of relative gradient [28] that uses the Lie
group structure of the ICA problem.
In the case of basic ICA, both of these principles amount to multiplying the
right-hand side of (36) by
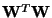 .
Thus we obtain
.
Thus we obtain
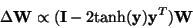 |
(37) |
with
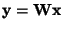 .
After this modification, the algorithm does not need sphering.
Interestingly, this algorithm is a special case of the
non-linear decorrelation algorithm in (34), and is closely
related to the algorithm in (35).
.
After this modification, the algorithm does not need sphering.
Interestingly, this algorithm is a special case of the
non-linear decorrelation algorithm in (34), and is closely
related to the algorithm in (35).
Finally, in [124], a Newton method for maximizing the
likelihood was introduced. The Newton method
converges in fewer iterations, but has the drawback that a matrix
inversion (at least approximate) is needed in every iteration.



Next: Non-linear PCA algorithms
Up: Algorithms for ICA
Previous: Non-linear decorrelation algorithms
Aapo Hyvarinen
1999-04-23
![]() .
Thus we obtain
.
Thus we obtain