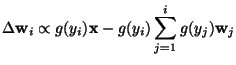Next: Neural one-unit learning rules
Up: Algorithms for ICA
Previous: Algorithms for maximum likelihood
Nonlinear extensions of the well-known neural PCA algorithms
[110,114,111]
were developed in [115].
For example, in [115], the following non-linear
version of a hierarchical PCA
learning rule was introduced:
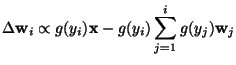 |
|
|
(38) |
where g is a suitable non-linear scalar function. The
symmetric versions of the learning rules in [114,111] can be
extended for the non-linear case in the same manner.
In [82], a connection between these algorithms and
non-linear versions of PCA criteria (see Section 4.3.4) were
proven. In general, the introduction of
non-linearities means that the learning rule uses higher-order
information in the learning. Thus, the learning rules may perform
something more related to the higher-order representation techniques
(projection pursuit, blind deconvolution, ICA).
In [84,112], it was proven that for well-chosen
non-linearities, the learning rule in (38) does indeed perform
ICA, if the data is sphered (whitened). Algorithms for
exactly maximizing the nonlinear PCA criteria were introduced in
[113].
An interesting simplification of the non-linear PCA algorithms is the
bigradient algorithm [145]. The feedback term in the learning
rule (38) is here
replaced by a much simpler one, giving
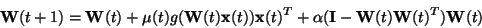 |
(39) |
where 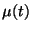 is the learning rate (step size) sequence,
is the learning rate (step size) sequence, 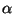 is a constant on the range [.5,1], the function g is applied
separately on every component of the vector
is a constant on the range [.5,1], the function g is applied
separately on every component of the vector
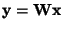 ,
and the data is
assumed to be sphered. A hierarchical version of the
bigradient algorithm is also possible. Due to the simplicity of the
bigradient algorithm, its properties can be analyzed in more
detail, as in [145] and [73].
,
and the data is
assumed to be sphered. A hierarchical version of the
bigradient algorithm is also possible. Due to the simplicity of the
bigradient algorithm, its properties can be analyzed in more
detail, as in [145] and [73].



Next: Neural one-unit learning rules
Up: Algorithms for ICA
Previous: Algorithms for maximum likelihood
Aapo Hyvarinen
1999-04-23