Projection pursuit

Projection pursuit [45,46,57,78,132,37] is a technique developed in statistics for finding 'interesting' projections of multidimensional data. Such projections can then be used for optimal visualization of the clustering structure of the data, and for such purposes as density estimation and regression. Reduction of dimension is also an important objective here, especially if the aim is visualization of the data.

In basic (1-D) projection pursuit, we try to find directions ${\bf w}$ such that the projection of the data in that direction, ${\bf w}^T{\bf x}$, has an 'interesting' distribution, i.e., displays some structure. It has been argued by Huber [57] and by Jones and Sibson [78] that the Gaussian distribution is the least interesting one, and that the most interesting directions are those that show the least Gaussian distribution.

The usefulness of finding such projections can be seen in Fig. 2, where the projection on the projection pursuit direction, which is horizontal, clearly shows the clustered structure of the data. The projection on the first principal component (vertical), on the other hand, fails to show this structure.

  

Figure 2: A classical illustration of the problems of variance-based methods like PCA. The data in this figure is clearly divided into two clusters. However, the principal component, i.e. the direction of maximum variance, would be vertical. Projections on the principal component would thus not produce any separation of clusters. In contrast, the projection pursuit direction is horizontal, providing optimal separation of the clusters.

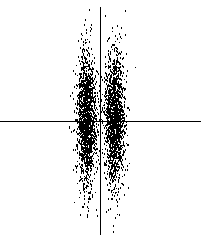In projection pursuit, one thus wants to reduce the dimension in such a way that some of the 'interesting' features of the data are preserved. This is in contrast to PCA where the objective is to reduce the dimension so that the representation is as faithful as possible in the mean-square sense.

The central theoretical problem in projection pursuit is the definition of the projection pursuit index that defines the 'interestingness' of a direction. Usually, the index is some measure of non-Gaussianity. A most natural choice is using differential entropy [57,78]. The differential entropy H of a random vector ${\bf y}$ whose density is f(.), is defined as:

$$H({\bf y})=-\int f({\bf y})\log f({\bf y})\mbox{d}{\bf y}$$ (6)

Now, consider zero-mean variables ${\bf y}$ of different densities f, and constrain the covariance of ${\bf y}$ to be fixed. Then the differential entropy $H({\bf y})$ is maximized with respect to f when f is a Gaussian density. For any other distribution, entropy is strictly smaller. Thus one might try to find projection pursuit directions by minimizing $H({\bf w}^T{\bf x})$ with respect to ${\bf w}$, constraining the variance of ${\bf w}^T{\bf x}$ to be constant.

The problem with differential entropy is that the estimation of entropy according to definition (6) requires estimation of the density of ${\bf w}^T{\bf x}$, which is difficult both in theory and in practice. Therefore, other measures of non-normality have been proposed [37,46]. These are based on weighted L² distances between the density of ${\bf x}$ and the multivariate Gaussian density. Another possibility is to use cumulant-based approximations of differential entropy [78]. Furthermore, in [64], approximations of negentropy based on the maximum entropy principle were introduced. More details can be found in Section 4.4.1.