

Next: About this document ...
Up: Fast and Robust Fixed-Point
Previous: Proof of convergence of
Appendix: Adaptive neural algorithms
Let us consider sphered data only. Taking the instantaneous gradient
of the approximation of negentropy
in (7) with respect to  ,
and taking the normalization
,
and taking the normalization
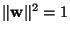 into account,
one obtains the following Hebbian-like learning rule
into account,
one obtains the following Hebbian-like learning rule
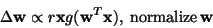 |
(38) |
where
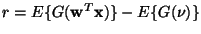 .
This is equivalent to the learning rule in [24], except
that the self-adaptation constant r is different.
.
This is equivalent to the learning rule in [24], except
that the self-adaptation constant r is different.
To find the whole n-dimensional transform
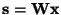 ,
one can
then use a network of n neurons, each of which learns according
to eq. (38).
Of course, some kind of feedback is then necessary.
In [24], it was shown how to add a bigradient
feedback to the learning rule. Denoting by
,
one can
then use a network of n neurons, each of which learns according
to eq. (38).
Of course, some kind of feedback is then necessary.
In [24], it was shown how to add a bigradient
feedback to the learning rule. Denoting by
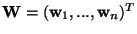 the weight matrix whose rows are the weight
vectors
the weight matrix whose rows are the weight
vectors 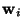 of the neurons, we obtain:
of the neurons, we obtain:
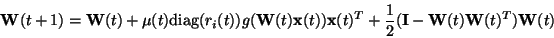 |
(39) |
where 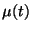 is the learning rate sequence,
and the function
g(.)=G'(.) is applied separately on every component of the
vector
is the learning rate sequence,
and the function
g(.)=G'(.) is applied separately on every component of the
vector
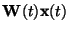 .
In this most general version of the learning rule,
the
ri, i=1...n are estimated separately for each neuron, as given
above (see also [24]). They may also be fixed using prior knowledge.
.
In this most general version of the learning rule,
the
ri, i=1...n are estimated separately for each neuron, as given
above (see also [24]). They may also be fixed using prior knowledge.


Next: About this document ...
Up: Fast and Robust Fixed-Point
Previous: Proof of convergence of
Aapo Hyvarinen
1999-04-23
![]() ,
and taking the normalization
,
and taking the normalization
![]() into account,
one obtains the following Hebbian-like learning rule
into account,
one obtains the following Hebbian-like learning rule
![]() ,
one can
then use a network of n neurons, each of which learns according
to eq. (38).
Of course, some kind of feedback is then necessary.
In [24], it was shown how to add a bigradient
feedback to the learning rule. Denoting by
,
one can
then use a network of n neurons, each of which learns according
to eq. (38).
Of course, some kind of feedback is then necessary.
In [24], it was shown how to add a bigradient
feedback to the learning rule. Denoting by
![]() the weight matrix whose rows are the weight
vectors
the weight matrix whose rows are the weight
vectors ![]() of the neurons, we obtain:
of the neurons, we obtain: