


Next: Appendix: Adaptive neural algorithms
Up: Appendix: Proofs
Previous: Proof of convergence of
Denote by 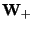 the result of applying
once the iteration step 2 in (26) on
the result of applying
once the iteration step 2 in (26) on 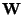 .
Let
.
Let
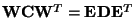 be the eigenvalue decomposition of
be the eigenvalue decomposition of
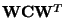 .
Then we have
.
Then we have
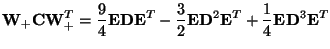 |
|
|
(35) |
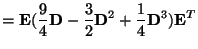 |
|
|
(36) |
Note that due to the normalization, i.e. division of 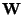 by
by
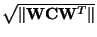 ,
all the eigenvalues of
,
all the eigenvalues of
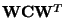 are in the interval [0,1].
Now, according to (35), for every eigenvalue
of
are in the interval [0,1].
Now, according to (35), for every eigenvalue
of
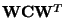 ,
say
,
say 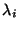 ,
,
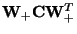 has a corresponding
eigenvalue
has a corresponding
eigenvalue
 where h(.) is defined as:
where h(.) is defined as:
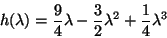 |
(37) |
Thus, after k iterations, the eigenvalues of
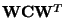 are obtained as
are obtained as
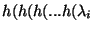 )))),
where h is applied k times on the
)))),
where h is applied k times on the 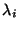 ,
which
are the eigenvalues of
,
which
are the eigenvalues of
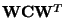 for the original matrix
before the iterations.
Now, we have always
for the original matrix
before the iterations.
Now, we have always
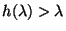 for
for
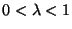 .
It is therefore clear that all the eigenvalues of
.
It is therefore clear that all the eigenvalues of
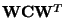 converge to 1, which means that
converge to 1, which means that
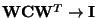 ,
Q.E.D.
Moreover, it is not difficult to see
that the convergence is quadratic.
,
Q.E.D.
Moreover, it is not difficult to see
that the convergence is quadratic.



Next: Appendix: Adaptive neural algorithms
Up: Appendix: Proofs
Previous: Proof of convergence of
Aapo Hyvarinen
1999-04-23
![]() the result of applying
once the iteration step 2 in (26) on
the result of applying
once the iteration step 2 in (26) on ![]() .
Let
.
Let
![]() be the eigenvalue decomposition of
be the eigenvalue decomposition of
![]() .
Then we have
.
Then we have