Perusalgoritmi

  Algoritmin jokaisella opetusaskeleella $t=1,2,3,\ldots,T$ otetaan opetusjoukosta satunnaisessa järjestyksessä datavektoreita $\bf x$. Datavektorille haetaan syöteavaruudessa lähin mallivektori ${\bf m}_c$, jolle siis pätee

$$\Vert {\bf x}-{\bf m}_c\Vert = \min _{i} \{\Vert {\bf x}-{\bf m}_i\Vert\}$$ (1)

Tätä mallivektoria vastaavaa karttayksikköä ${\bf n}_c$ kutsutaan voittajayksiköksi.

Voittajayksikön ja sen naapuruston mallivektoreita päivitetään seuraavasti:

 

$${\bf{m}}_{i}(t+1)={\bf{m}}_{i}(t)+h_{ci}(t)[{\bf{x}}(t)-{\bf{m}}_i(t)]$$ (2)

Funktio h_ci on naapurustokernel, jonka on oltava vähenevä ajan (opetusaskelten) suhteen, jotta algoritmi konvergoituisi. Naapurustokernel on oppimisnopeuskertoimen ($\alpha$) ja naapurustofunktion (h) tulo $h_{ci}=\alpha(t) h(c,i;t)$.

Oppimisnopeuskerroin $\alpha$ on yleensä joko lineaarisesti tai funktion

 

$$\alpha(t)=\frac{A}{t+B}$$ (3)

mukaisesti ajan suhteen vähenevä. Lisäksi vaaditaan, että $0<\alpha<1$.

Naapurustofunktioksi h voidaan valita esimerkiksi kuplanaapurusto:

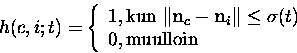$$h(c,i; t)=\left\{ \begin{array} {ll} 1, \mbox{kun $ \Vert{\b... ...eq \sigma(t) $\space } \\ 0, \mbox{muulloin}\end{array}\right.$$ (4)

tai gaussinen naapurusto:

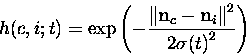$$h(c,i; t)=\exp\left(-\frac{{\Vert{\bf n}_c - {\bf n}_i \Vert}^2}{2 {\sigma(t)}^2}\right)$$ (5)

On esitetty, että naapurustofunktion konveksisuudesta on etua (ks. luku 2.2.5). Gaussisesta naapurustofunktiosta voidaan leikata konkaavit hännät pois, jolloin saadaan katkaistu gaussinen naapurustofunktio.

$$h(c,i; t)=\left\{ \begin{array} {ll} \exp\left(-\frac{{\Vert... ...eq \sigma(t) $\space } \\ 0, \mbox{muulloin}\end{array}\right.$$ (6)

Myös Epanechnikovin kernel, (esim. [5, sivu 149]) on konveksi ja täyttää naapurustofunktion ehdot:

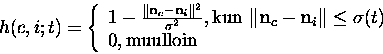$$h(c,i; t)=\left\{ \begin{array} {ll} 1-\frac{\Vert{\bf n}_c ... ...eq \sigma(t) $\space } \\ 0, \mbox{muulloin}\end{array}\right.$$ (7)

Opetusjoukko käydään yleensä läpi useita kertoja, jotta saataisiin riittävä määrä opetusaskelia. Yhtä opetusjoukon läpikäyntiä kutsutaan epokiksi.