Jonon parametreja

Asiakkaat C_n saapuvat jonoon ajanhetkillä $\tau_n$. Saapumisten väliset ajat ovat siten $t_n=\tau_n-\tau_{n-1}$. Usein oletetaan, että t_n on peräisin satunnaisjakautumasta, jonka kertymäfunktio olkoon A(t). Asiakkaan C_n palveluaika x_n on puolestaan peräisin satunnaisjakautumasta B(x). Jonon pituutta merkitään N_Q(t):llä ja palvelijoiden määrää s:llä. Asiakkaan C_n odotusaika - eli jonossa vietetty aika - on puolestaan w_n.

Yksinkertaisimmissa malleissa oletetaan, että A(t) ja B(x) eivät riipu jonotussysteemin tilasta tai ajanhetkestä $\tau$, mikä ei tietenkään pidä aina paikkaansa reaalimaailmassa. Jos esimerkiksi ruokalan jono kasvaa, alkaa usein saapumisten väliaika pidentyä, kun ihmiset valitsevat jonkin vähemmän ruuhkaisen paikan. Ruuhkaisessa palvelussa taas esimerkiksi palveluaika voi lyhetä tehokkuuden kasvaessa, tai kasvaa, jos palvelija rasituksen vuoksi ei voi toimia enää tehokkaasti. Sen lisäksi saapumis- ja palveluprosessi riippuvat käytännössä tietysti myös lukuisista muista tekijöistä. Ruokalan asiakkaiden saapuminen on varmaankin selkeästi kytköksissä kellonaikaan, viikonpäivään ja ruokalistaan.

Määritellään keskimääräinen saapumisten välinen aika ja keskimääräinen palveluaika. Koska oletetaan, että kaikki t_n ja x_n ovat peräisin samoista jakautumista, merkitään yksinkertaisesti $\overline{t}=E[t_n]$ ja $\overline{x}=E[x_n]$. Määritellään keskimääräinen saapumisintensiteetti $\lambda=\frac{1}{\overline{t}}$. Samoin saadaan keskimääräinen palveluintensiteetti $\mu=\frac{1}{\overline{x}}$. Näiden parametrien avulla voidaan määritellä systeemin liikenneintensiteetti $\alpha$:

 

$$\alpha=\frac{\lambda}{\mu}$$ (16)

ja käyttöaste $\rho$ 

$$\rho=\frac{\alpha}{s}$$ (17)

Jotta jono pysyisi pitkällä aikavälillä äärellisenä on käyttöasteen oltava alle yksi; muuten jono kasvaa rajatta.

Jonotusjärjestelmiä kuvataan esimerkiksi seuraavilla merkintätavoilla

A/B/s/K/M, tai lyhyemmin
A/B/s,

jossa A on saapumisten ja B palveluaikojen väliaikojen jakautuma. Jakautumista käytetään yleisesti symboleita eksponentiaalinen (M), Erlang-jakautuma (E_r), hypereksponentiaalinen jakautuma (H_R), ei-satunnainen eli deterministinen jakautuma (D) ja yleinen jakautuma (G).

Merkinnän pidemmässä muodossa K kuvaa jonotuspaikkojen määrää ja M potentiaalisten jonottajien populaatiota. Jos jälkimmäiset on jätetty pois, ne oletetaan äärettömiksi, ts. M/M/s tarkoittaa samaa kuin $M/M/s/\infty/\infty$. M/M/s-jono on yksinkertainen jonomalli, joka suurin piirtein kuvaa tässä työssä käsiteltävää järjestelmää. Mallille voidaan johtaa tasapainotilassa keskimääräinen jonon pituus N_Q:

 

$$N_{Q}=\frac{\lambda}{s\mu-\lambda} C(\alpha,s),$$ (18)

jossa  

$$C(\alpha,s)=\frac{1}{1-\rho}\frac{\alpha^{s}}{s!}\frac{1}{C_{0}}$$ (19)

on ns. Erlangin C-funktio, jossa  

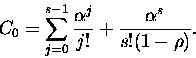$$C_{0}=\sum_{j=0}^{s-1}\frac{\alpha^{j}}{j!}+\frac{\alpha^{s}}{s!(1-\rho)}.$$ (20)

Keskimääräinen jonotusaika W_Q voidaan laskea tästä jonoteoriassa keskeisen Littlen kaavan avulla

 

$$W_{Q}=\frac{N_Q}{\lambda}$$ (21)

eli keskimääräinen jonon pituus tasapainotilassa on saapumisintensiteetti kertaa keskimääräinen odotusaika.