


Next: Proof of convergence of
Up: Appendix: Proofs
Previous: Appendix: Proofs
The convergence is proven under the assumptions that first, the data follows
the ICA data model (2) and second, that the expectations are
evaluated exactly.
We must also make the following technical assumption:
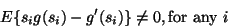 |
(27) |
which can be considered a generalization
of the condition, valid when we use kurtosis as contrast,
that the kurtosis of the independent components must be non-zero.
If (27) is true for a subset of independent components, we can estimate just those independent components.
To begin with, make the change of variable
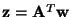 ,
as above, and assume that
,
as above, and assume that 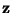 is
in the neighbourhood
of a solution (say,
is
in the neighbourhood
of a solution (say,
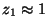 as above).
As shown in proof of Theorem 1 (see [24]), the change in z1 is then of
a lower order than the change in the other coordinates, due to the
constraint
as above).
As shown in proof of Theorem 1 (see [24]), the change in z1 is then of
a lower order than the change in the other coordinates, due to the
constraint
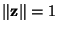 .
Then we can expand the terms in (20) using a Taylor approximation
for g and g', first obtaining
.
Then we can expand the terms in (20) using a Taylor approximation
for g and g', first obtaining
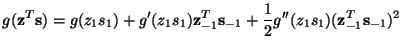 |
|
|
(28) |
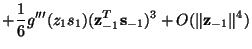 |
|
|
(29) |
and then
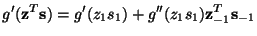 |
|
|
(30) |
 |
|
|
(31) |
where
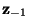 and
and
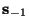 are the vectors
are the vectors 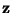 and
and 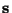 without their first components.
Thus we obtain, using the independence of the si, and doing some
tedious but straight-forward algebraic manipulations,
without their first components.
Thus we obtain, using the independence of the si, and doing some
tedious but straight-forward algebraic manipulations,
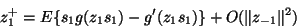 |
(32) |
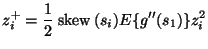 |
|
|
|
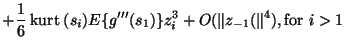 |
|
|
(33) |
We obtain also
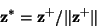 |
(34) |
This shows clearly that
under the assumption (27), the algorithm
converges (locally) to such a vector 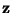 that
that 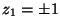 and zi=0 for i>1.
This means that
and zi=0 for i>1.
This means that
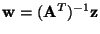 converges, up to the sign,
to one of the rows of the
inverse of the mixing matrix
converges, up to the sign,
to one of the rows of the
inverse of the mixing matrix 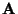 ,
which implies that
,
which implies that
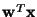 converges to one of the si.
Moreover, if
converges to one of the si.
Moreover, if
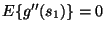 ,
i.e. if the si has a symmetric
distribution, as is usually the case,
(33) shows that the convergence is cubic.
In other cases, the convergence is quadratic.
In addition, if G(u)=u4, the local approximations above are exact, and the
convergence is global.
,
i.e. if the si has a symmetric
distribution, as is usually the case,
(33) shows that the convergence is cubic.
In other cases, the convergence is quadratic.
In addition, if G(u)=u4, the local approximations above are exact, and the
convergence is global.



Next: Proof of convergence of
Up: Appendix: Proofs
Previous: Appendix: Proofs
Aapo Hyvarinen
1999-04-23
![]() ,
as above, and assume that
,
as above, and assume that ![]() is
in the neighbourhood
of a solution (say,
is
in the neighbourhood
of a solution (say,
![]() as above).
As shown in proof of Theorem 1 (see [24]), the change in z1 is then of
a lower order than the change in the other coordinates, due to the
constraint
as above).
As shown in proof of Theorem 1 (see [24]), the change in z1 is then of
a lower order than the change in the other coordinates, due to the
constraint
![]() .
Then we can expand the terms in (20) using a Taylor approximation
for g and g', first obtaining
.
Then we can expand the terms in (20) using a Taylor approximation
for g and g', first obtaining