Virhemittoja

 Yksinkertaisin mittari kartan erottelukyvyn mittaamiseksi on keskimääräinen kvantisointivirhe $\epsilon_q$:

 

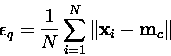$$\epsilon_{q}=\frac{1}{N}\sum_{i=1}^{N}\Vert{\bf{x}}_{i}-{\bf{m}}_{c}\Vert$$ (8)

Kahden kartan vertaaminen toisiinsa kvantisointivirheen avulla ei ole aina järkevää, sillä suuremmalla kartalla voidaan tietysti kvantisoida opetusjoukko tarkemmin. Samoin on ilmeistä, että pienempi naapuruston säde opetuksessa tuottaa usein tarkemman kvantisoinnin, sillä mallivektorit voivat liikkua toisistaan suuremmin välittämättä. Vasta samankokoisten ja samalla naapurustofunktiolla opetettujen karttojen vertailu on mielekästä [24].

Data on yleensä korkeampiulotteista kuin kartan hilarakenne, siis $d_{\mathcal D} \gt d_{\mathcal L}$. Kartta pyrkii tällöin mallintamaan datajoukkoa laskostumalla kuten kuvassa 2.2.

Kartan laskostumattomuuden eli kuvauksen jatkuvuuden merkitys on tärkeä esimerkiksi visualisoinnin kannalta: repaleinen kuvaus ei kerro kartan tulkitsijalle selkeästi näytteiden keskinäisistä suhteista, ja virhetulkintojen mahdollisuus kasvaa. Kuvauksen jatkuvuutta kuvataan topografisella virheellä $\epsilon_t$. Tämän työn yhdessä aihepiirissä, prosessien monitoroinnissa, on topografinen virhe todettu tärkeäksi ongelmaksi [19].

Esimerkkinä tarkastellaan kahta kaksiulotteista karttaa, jotka on opetettu samalla yksikkökuutioon tasan jakautuneella pseudosatunnaisdatalla. Molemmat kartat on alustettu samoin (kuva 2.2(a)). Kartta kuvassa 2.2(b) on järjestynyt. Se täyttää kartan topologian säilyttävän ominaisuuden paremmin kuin kuvan 2.2(c) kartta, mutta sen kvantisointivirhe jää suuremmaksi. Jälkimmäinen kartta on puolestaan voimakkaammin laskostunut, jolloin lähellä toisiaan olevat datavektorit kuvautuvat useammin hilassa toisistaan kaukana oleviin karttayksiköihin.

Topografisia virhemittoja on ehdotettu useita. Yhteenvetoja löytyy esimerkiksi lähteistä [18,41]. Yksinkertainen topografinen virhemitta on Kiviluodon esittämä [20]. Lasketaan kullekin datavektorille ${\bf x}_i$ kaksi lähintä yksikköä ${\bf n}_{c1}^i$ ja ${\bf n}_{c2}^i$. Lasketaan kuinka monen datavektorin voittajayksikköparit ${\bf n}_{c1}^i$ ja ${\bf n}_{c2}^i$ eivät ole toistensa välittömiä naapureita hilassa. Virhemitta on tämän määrän suhde datavektorien määrään, siis:

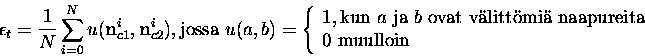$$\epsilon_{t}=\frac{1}{N}\sum_{i=0}^N u({\bf n}_{c1}^i,{\bf n... ...välittömiä naapureita } \\ 0 \mbox{ muulloin}\end{array}\right.$$ (9)

Yksinkertaisuuden lisäksi tämän mitan etu on erilaisten karttojen ja datajoukkojen virheitten vertailukelpoisuus [42], koska karttojen koko, datan määrä ja muut parametrit eivät selvästikään vaikuta tämän virhemitan skaalaan.

     

Figure: Kuvan kartat (23$\times$21 yksikköä, kuusikulmionaapurusto, gaussinen naapurustofunktio) on opetettu yksikkökuutioon tasan jakautuneella 3000 näytteen pseudosatunnaisdatalla. Virheet on laskettu samoin jakautuneella riippumattomalla testijoukolla.

Kaski ja Lagus ovat ehdottaneet yhdistettyä mittaa, topografista kvantisointivirhettä $\epsilon_{tq}$, jossa erottelykyvyn ja jatkuvuuden mitat yhdistetään [18]. Mitta on summa kahdesta etäisyydestä: Lasketaan syötevektorin etäisyys voittajayksikköön ${\bf n}_{c1}$, siis kvantisointivirhe. Tähän lisätään lyhin mahdollinen etäisyys $d=\Vert{\bf n}_{c1}-{\bf n}_{c2}\Vert$ niistä etäisyyksistä, jotka saadaan ${\bf n}_{c1}$ ja ${\bf n}_{c2}$ välille aina vierekkäisestä yksiköstä toiseen kulkien. Kartan yhdistetty virhe datajoukon suhteen on datajoukon vektoreiden virheiden keskiarvo. Toisin sanoen (viitteen [41] merkintätapaa mukaellen)

 

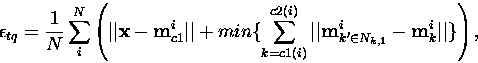$$\epsilon_{tq} = \frac{1}{N} \sum_i^N \left( \vert\vert{\bf ... ...\bf m}_{k' \in N_{k,1}}^i - {\bf m}_k^i \vert\vert \} \right),$$ (10)

jossa k korvataan k':lla jokaisen summausaskeleen jälkeen. N_k,1 tarkoittaa yksikön ${\bf n}_k$ lähimpiä naapureita hilassa.